题目内容
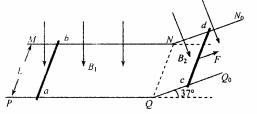
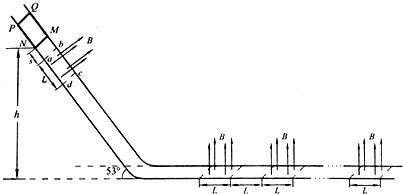
如图所示,两条光滑的绝缘导轨,导轨的水平部分与倾斜部分平滑连接.两导轨间距为L=0.5m.导轨的倾斜部分与水平面成θ=530角.其中有一段匀强磁场区域abcd,磁场方向垂直于斜面向上.导轨的水平部分有n段相同的匀强磁场区域.磁场方向竖直向上,所有磁场的磁感虚强度大小均为B=1T.磁场沿导轨的长度均为L=0.5m.磁场左、右两侧边界均与导轨垂直.导轨的水平部分中相邻磁场区域的间距也为L.现有一质量为m=0.5kg,电阻为r=0.125Ω,边长也为L的正方形金属框PQMN,从倾斜导轨上由静止释放,释放时MN边离水平导轨的高度h=2.4m,金属框滑进磁场abcd时恰好作匀速运动,此后,金属框从导轨的倾斜部分滑上水平部分并最终停停止.取重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.求:
(1)金属框刚释放时MN边与ab的距离s;
(2)金属框能穿过导轨的水平部分中几段磁场区域;
(3)整个过程中金属框内产生的电热.
(1)金属框刚释放时MN边与ab的距离s;
(2)金属框能穿过导轨的水平部分中几段磁场区域;
(3)整个过程中金属框内产生的电热.

(1)设金属线框刚进入磁场区域abcd的速度为v1,则线框中产生的感应电动势E=BLv1
安培力F=BIL=
依题意金属框滑进磁场abcd时恰好作匀速运动,有:F=mgsinθ
线框下滑距离s的过程中,根据动能定理,有:mgssinθ=
mv12
联立以上各式解得:s=
gsinθ=0.25m
(2)设金属线框刚全部进入水平导轨时速度为v2,线框在倾斜轨道上运动的全过程中,根据动能定理,有:
mg(h+
Lsinθ-2Lsinθ)=
mv2
解得:v2=6m/s
线框进入水平导轨的磁场中后由于受到安培力作用而减速直至速度减为零,线框在穿越任一磁场区域的过程中,根据动量定理,有:B
Lt=m△v,即BLq=m△v
又q=
=
所以,线框在穿越每一磁场区域速度的减少量相同,且△v=
线框在水平导轨上穿越磁场区域的个数
n=
=
=1.5
金属框能穿越导轨水平部分中1个完整的磁场区域.
(3)整个过程中,根据能量守恒定律,有:
金属线框内产生的焦耳热Q=mg(h+
Lsinθ)=13J.
答:(1)金属线框刚释放时MN边与ab的距离S是0.25m
(2)整个过程中金属线框内产生的焦耳热是13 J.
(3)金属线框能穿越导轨水平部分中1个完整的磁场区域.
安培力F=BIL=
| B2L2v1 |
| r |
依题意金属框滑进磁场abcd时恰好作匀速运动,有:F=mgsinθ
线框下滑距离s的过程中,根据动能定理,有:mgssinθ=
| 1 |
| 2 |
联立以上各式解得:s=
| m2r2 |
| 2B4L4 |
(2)设金属线框刚全部进入水平导轨时速度为v2,线框在倾斜轨道上运动的全过程中,根据动能定理,有:
mg(h+
| 1 |
| 2 |
| 1 |
| 2 |
解得:v2=6m/s
线框进入水平导轨的磁场中后由于受到安培力作用而减速直至速度减为零,线框在穿越任一磁场区域的过程中,根据动量定理,有:B
| . |
| I |
又q=
| △φ |
| r |
| 2BL2 |
| r |
所以,线框在穿越每一磁场区域速度的减少量相同,且△v=
| 2B2L3 |
| mr |
线框在水平导轨上穿越磁场区域的个数
n=
| v2-0 |
| △v |
| mrv2 |
| 2B2L3 |
金属框能穿越导轨水平部分中1个完整的磁场区域.
(3)整个过程中,根据能量守恒定律,有:
金属线框内产生的焦耳热Q=mg(h+
| 1 |
| 2 |
答:(1)金属线框刚释放时MN边与ab的距离S是0.25m
(2)整个过程中金属线框内产生的焦耳热是13 J.
(3)金属线框能穿越导轨水平部分中1个完整的磁场区域.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
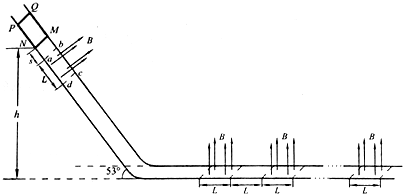
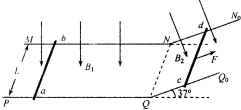 如图所示,两条光滑的金属导轨相距L=lm,其中MN段平行于PQ段,位于同一水平面内,NN0段与QQ0段平行,位于与水平面成倾角37°的斜面内,且MNN0与PQQ0均在竖直平面内.在水平导轨区域和倾斜导轨区域内分别有垂直于水平面和斜面的匀强磁场B1和B2,且B1=B2=0.5T.ab和cd是质量均为m=0.1kg、电阻均为R=4Ω的两根金属棒,ab置于水平导轨上,ab置于倾斜导轨上,均与导轨垂直且接触良好.从t=0时刻起,ab棒在外力作用下由静止开始沿水平方向向右运动(ab棒始终在水平导轨上运动,且垂直于水平导轨),cd受到F=0.6-0.25t(N)沿斜面向上的力的作用,始终处于静止状态.不计导轨的电阻.(sin37°=0.6)
如图所示,两条光滑的金属导轨相距L=lm,其中MN段平行于PQ段,位于同一水平面内,NN0段与QQ0段平行,位于与水平面成倾角37°的斜面内,且MNN0与PQQ0均在竖直平面内.在水平导轨区域和倾斜导轨区域内分别有垂直于水平面和斜面的匀强磁场B1和B2,且B1=B2=0.5T.ab和cd是质量均为m=0.1kg、电阻均为R=4Ω的两根金属棒,ab置于水平导轨上,ab置于倾斜导轨上,均与导轨垂直且接触良好.从t=0时刻起,ab棒在外力作用下由静止开始沿水平方向向右运动(ab棒始终在水平导轨上运动,且垂直于水平导轨),cd受到F=0.6-0.25t(N)沿斜面向上的力的作用,始终处于静止状态.不计导轨的电阻.(sin37°=0.6)