题目内容
如图所示,两条光滑的绝缘导轨,导轨的水平部分与圆弧部分平滑连接,两导轨间距为L,导轨的水平部分有n段相同的匀强磁场区域(图中的虚线范围),磁场方向竖直向上,磁场的磁感应强度为B,磁场的宽度为S,相邻磁场区域的间距也为S,S大于L,磁场左、右两边界均与导轨垂直.现有一质量为m,电阻为r,边长为L的正方形金属框,由圆弧导轨上某高度处静止释放,金属框滑上水平导轨,在水平导轨上滑行一段时间进入磁场区域,最终线框恰好完全通过n段磁场区域.地球表面处的重力加速度为g,感应电流的磁场可以忽略不计,求:
(1)刚开始下滑时,金属框重心离水平导轨所在平面的高度.
(2)整个过程中金属框内产生的电热.
(3)金属框完全进入第k(k<n)段磁场区域前的时刻,金属框中的电功率.
(1)刚开始下滑时,金属框重心离水平导轨所在平面的高度.
(2)整个过程中金属框内产生的电热.
(3)金属框完全进入第k(k<n)段磁场区域前的时刻,金属框中的电功率.

分析:(1)金属框从光滑导轨下滑的过程中,机械能守恒,要求高度,关键要求出金属框在进入第一段匀强磁场区域前的速度v0,可根据法拉第定律、欧姆定律和动量定理,对线框进入第一段、第二段、第三段…磁场区域列式,再累计求和,即可求出v0,再根据机械能守恒求解高度.
(2)金属框穿过第(k-1)个磁场区域后和完全进入第k个磁场区域的过程中,由动量定理求得速度,即可求出电功率.
(2)金属框穿过第(k-1)个磁场区域后和完全进入第k个磁场区域的过程中,由动量定理求得速度,即可求出电功率.
解答:解:(1)设金属框在进入第一段匀强磁场区域前的速度为v0,金属框在进入和穿出第一段匀强磁场区域的过程中,线框中产生平均感应电动势为
=
平均电流强度为(不考虑电流方向变化)
=
=
由动量定理得:
-B
Lt=mv1-mv0
-B
Lt=mv1-mv0
-
=mv1-mv0
同理可得:-
=mv2-mv1
-
=mv3-mv2
…
整个过程累计得:-n
=0-mv0
解得:v0=
金属框沿斜面下滑机械能守恒:mgh=
m
解得 h=
=
(2)金属框中产生的热量Q=mgh,
解得 Q=
(3)金属框穿过第(k-1)个磁场区域后,由动量定理得:-(k-1)
=mvk-1-mv0
金属框完全进入第k个磁场区域的过程中,由动量定理得:-
=mvk′-mvk-1
解得:vk′=
金属框中的电功率:P=
=
答:
(1)刚开始下滑时,金属框重心离水平导轨所在平面的高度是
.
(2)整个过程中金属框内产生的电热是
.
(3)金属框完全进入第k(k<n)段磁场区域前的时刻,金属框中的电功率是
.
. |
| E |
| 2BL2 |
| t |
平均电流强度为(不考虑电流方向变化)
. |
| I |
| ||
| r |
| 2BL2 |
| rt |
由动量定理得:
-B
. |
| I |
-B
| 2BL2 |
| rt |
-
| 2B2L3 |
| r |
同理可得:-
| 2B2L3 |
| r |
-
| 2B2L3 |
| r |
…
整个过程累计得:-n
| 2B2L3 |
| r |
解得:v0=
| 2nB2L3 |
| mr |
金属框沿斜面下滑机械能守恒:mgh=
| 1 |
| 2 |
| v | 2 0 |
解得 h=
| ||
| 2g |
| 2n2B4L6 |
| m2gr2 |
(2)金属框中产生的热量Q=mgh,
解得 Q=
| 2n2B4L6 |
| mr2 |
(3)金属框穿过第(k-1)个磁场区域后,由动量定理得:-(k-1)
| 2B2L3 |
| r |
金属框完全进入第k个磁场区域的过程中,由动量定理得:-
| B2L3 |
| r |
解得:vk′=
| (2n-2k+1)B2L3 |
| mr |
金属框中的电功率:P=
(BL
| ||
| r |
| (2n-2k+1)2B6L8 |
| m2r3 |
答:
(1)刚开始下滑时,金属框重心离水平导轨所在平面的高度是
| 2n2B4L6 |
| mr2 |
(2)整个过程中金属框内产生的电热是
| 2n2B4L6 |
| mr2 |
(3)金属框完全进入第k(k<n)段磁场区域前的时刻,金属框中的电功率是
| (2n-2k+1)2B6L8 |
| m2r3 |
点评:本题综合考查了机械能守恒定律、能量守恒定律、法拉第电磁感应定律、闭合电路欧姆定律等,综合性较强,对学生能力要求较高,需加强这方面的训练.

练习册系列答案
相关题目

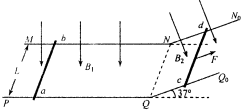 如图所示,两条光滑的金属导轨相距L=lm,其中MN段平行于PQ段,位于同一水平面内,NN0段与QQ0段平行,位于与水平面成倾角37°的斜面内,且MNN0与PQQ0均在竖直平面内.在水平导轨区域和倾斜导轨区域内分别有垂直于水平面和斜面的匀强磁场B1和B2,且B1=B2=0.5T.ab和cd是质量均为m=0.1kg、电阻均为R=4Ω的两根金属棒,ab置于水平导轨上,ab置于倾斜导轨上,均与导轨垂直且接触良好.从t=0时刻起,ab棒在外力作用下由静止开始沿水平方向向右运动(ab棒始终在水平导轨上运动,且垂直于水平导轨),cd受到F=0.6-0.25t(N)沿斜面向上的力的作用,始终处于静止状态.不计导轨的电阻.(sin37°=0.6)
如图所示,两条光滑的金属导轨相距L=lm,其中MN段平行于PQ段,位于同一水平面内,NN0段与QQ0段平行,位于与水平面成倾角37°的斜面内,且MNN0与PQQ0均在竖直平面内.在水平导轨区域和倾斜导轨区域内分别有垂直于水平面和斜面的匀强磁场B1和B2,且B1=B2=0.5T.ab和cd是质量均为m=0.1kg、电阻均为R=4Ω的两根金属棒,ab置于水平导轨上,ab置于倾斜导轨上,均与导轨垂直且接触良好.从t=0时刻起,ab棒在外力作用下由静止开始沿水平方向向右运动(ab棒始终在水平导轨上运动,且垂直于水平导轨),cd受到F=0.6-0.25t(N)沿斜面向上的力的作用,始终处于静止状态.不计导轨的电阻.(sin37°=0.6)
