题目内容
1. 如图所示,杆长为l,球的质量为m,杆连球在竖直平面内绕轴O自由转动,已知在最高点处,杆对球的弹力大小为$F=\frac{1}{2}mg$,求这时小球的瞬时速度大小.
如图所示,杆长为l,球的质量为m,杆连球在竖直平面内绕轴O自由转动,已知在最高点处,杆对球的弹力大小为$F=\frac{1}{2}mg$,求这时小球的瞬时速度大小.
分析 由题:杆在高点处,球的重力与杆的弹力的合力提供球的向心力,杆对球的弹力大小为$F=\frac{1}{2}mg$,由于F<mg,其方向可能向上,也可能向下.根据牛顿第二定律列方程求解速度.
解答 解:杆在高点处,球的重力与杆的弹力的合力提供球的向心力,根据牛顿第二定律,得
(1)若F向上,则mg-F=m$\frac{{v}^{2}}{l}$
解得v=$\sqrt{\frac{gl}{2}}$
(2)若F向下,则mg+F=m$\frac{{v}^{2}}{l}$
解得v=$\sqrt{\frac{3gl}{2}}$
答:小球的瞬时速度大小可能为$\sqrt{\frac{gl}{2}}$或$\sqrt{\frac{3gl}{2}}$.
点评 对于竖直平面内的圆周运动,轻杆与轻绳模型不同,在最高点时,绳对物体只有向下的拉力,而杆对物体可能施加向下拉力,也可能施加向上的支持力.

练习册系列答案
相关题目
15. 一物体由静止开始沿直线运动,其0~40s的加速度随时间变化如图所示,若从出发开始计时,则在40s内下列说法正确的是( )
一物体由静止开始沿直线运动,其0~40s的加速度随时间变化如图所示,若从出发开始计时,则在40s内下列说法正确的是( )
 一物体由静止开始沿直线运动,其0~40s的加速度随时间变化如图所示,若从出发开始计时,则在40s内下列说法正确的是( )
一物体由静止开始沿直线运动,其0~40s的加速度随时间变化如图所示,若从出发开始计时,则在40s内下列说法正确的是( )| A. | 10s与30s时速度方向相反 | B. | 20s时速度为零 | ||
| C. | 40s时物体返回出发点 | D. | 40s时,物体离出发点最远 |
13.下列说法中正确的是( )
| A. | 第1s初到第2s初表示经历了2s的时间 | |
| B. | 第3s内指的是3s的时间 | |
| C. | 第ns和第1s都是指1s的时间 | |
| D. | 在时间轴上,每一点代表时刻,每一段线段代表时间间隔 |
20.某人骑自行车沿一斜坡从坡底到坡顶,再从坡顶到坡底往返一次,已知上坡时的平均速度大小为4m/s,下坡时的平均速度大小为6m/s,则此人往返一次的平均速度大小是( )
| A. | 10 m/s | B. | 5 m/s | C. | 4.8 m/s | D. | 0 |
10.如图所示为一物体做直线运动的速度-时间图象,则下列说法正确的是( )
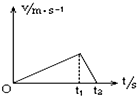

| A. | 0-t1时间内速度逐渐增大 | B. | t1-t2时间内速度逐渐减小 | ||
| C. | 0-t1时间内加速度逐渐减小 | D. | t1-t2时间内加速度保持不变 |
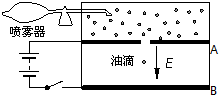 密立根油滴实验装置如图所示,已知A、B板间距离d为50mm,电源电压U为150V.当开关S断开,在电介质为空气的电容器中,观察以某速度进入的一个带电的油滴,这个油滴经过一会儿达到一个恒定的速度v0匀速下落.然后闭合开关S,则油滴经过一段时间后匀速上升,其速度大小也是v0.已测得油滴直径为1.01×10-6m,密度ρ为1.05×103kg/m3.已知空气阻力f和速度v0成正比,即f=kv0,空气浮力不计,元电荷e=1.6×10-19C.
密立根油滴实验装置如图所示,已知A、B板间距离d为50mm,电源电压U为150V.当开关S断开,在电介质为空气的电容器中,观察以某速度进入的一个带电的油滴,这个油滴经过一会儿达到一个恒定的速度v0匀速下落.然后闭合开关S,则油滴经过一段时间后匀速上升,其速度大小也是v0.已测得油滴直径为1.01×10-6m,密度ρ为1.05×103kg/m3.已知空气阻力f和速度v0成正比,即f=kv0,空气浮力不计,元电荷e=1.6×10-19C. 如图所示,质量为M、倾角为θ的斜面放在水平地面上,斜面上有一质量为m的滑块沿斜面以加速度a加速下滑,若斜面始终保持静止,求:
如图所示,质量为M、倾角为θ的斜面放在水平地面上,斜面上有一质量为m的滑块沿斜面以加速度a加速下滑,若斜面始终保持静止,求: