题目内容
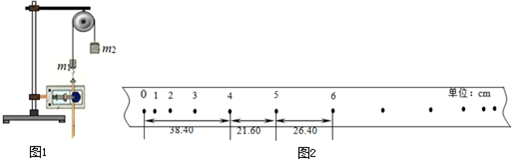
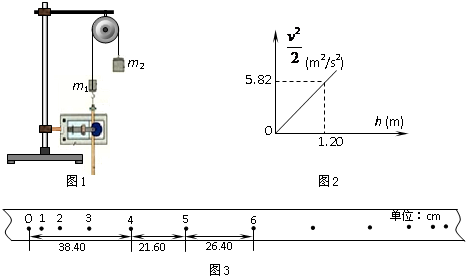
用如图1实验装置验证m1、m2组成的系统机械能守恒．m2从高处由静止开始下落，m1上拖着的纸带打出一系列的点，对纸带上的点迹进行测量，即可验证机械能守恒定律．如图3给出的是实验中获取的一条纸带：0是打下的第一个点，每相邻两计数点间还有4个点（图中未标出），计数点间的距离如图3所示．已知交流电频率f=50Hz，m1=50g、m2=150g，则（g取10m/s2，结果保留两位有效数字）
（1）在打点0～5过程中系统动能的增量△EK=
（2）若某同学作出
v2-h图象如图2，则当地的实际重力加速度g=
（1）在打点0～5过程中系统动能的增量△EK=
0.58
0.58
J，系统势能的减少量△EP=0.60
0.60
J，（2）若某同学作出
| 1 | 2 |
9.7
9.7
m/s2．分析：解决实验问题首先要掌握该实验原理，了解实验的仪器、操作步骤和数据处理以及注意事项．
纸带法实验中，若纸带匀变速直线运动，测得纸带上的点间距，利用匀变速直线运动的推论，可计算出打出某点时纸带运动的瞬时速度和加速度，从而求出动能．根据功能关系得重力势能减小量等于重力做功的数值．
对于物理量线性关系图象的应用我们要从两方面：1、从物理角度找出两变量之间的关系式2、从数学角度找出图象的截距和斜率，两方面结合解决问题．
纸带法实验中，若纸带匀变速直线运动，测得纸带上的点间距，利用匀变速直线运动的推论，可计算出打出某点时纸带运动的瞬时速度和加速度，从而求出动能．根据功能关系得重力势能减小量等于重力做功的数值．
对于物理量线性关系图象的应用我们要从两方面：1、从物理角度找出两变量之间的关系式2、从数学角度找出图象的截距和斜率，两方面结合解决问题．
解答：解：（1）利用匀变速直线运动的推论
v5=
=
m/s=2.4m/s．
系统动能的增量△EK=Ek5-0=
(m1+m2)v52=0.58J．
系统重力势能减小量△Ep=（m2-m1）gh=0.1×10×0.6000m J=0.60J．
（2）根据系统机械能守恒定律得，(m2-m1)gh=
(m1+m2)v2，解得
=
gh知图线的斜率k=
g=
．解得g=9.7m/s2．
故答案为：（1）0.58，0.60；（2 ）9.7．
v5=
| x46 |
| t46 |
| 0.2160+0.2640 |
| 0.2 |
系统动能的增量△EK=Ek5-0=
| 1 |
| 2 |
系统重力势能减小量△Ep=（m2-m1）gh=0.1×10×0.6000m J=0.60J．
（2）根据系统机械能守恒定律得，(m2-m1)gh=
| 1 |
| 2 |
| v2 |
| 2 |
| m2-m1 |
| m1+m2 |
| m2-m1 |
| m1+m2 |
| 5.8 |
| 12 |
故答案为：（1）0.58，0.60；（2 ）9.7．
点评：解决本题的关键掌握该实验的原理，能够根据系统机械能守恒定律得出图线斜率的意义，从而求出重力加速度的大小．
练习册系列答案
相关题目
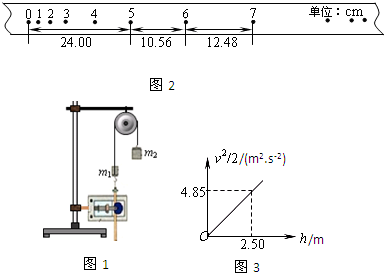用如图1实验装置验证m1、m2组成的系统机械能守恒．m2从高处由静止开始下落，m1上拖着的纸带打出一系列的点，对纸带上的点迹进行测量，即可验证机械能守恒定律．下图给出的是实验中获取的一条纸带：0是打下的第一个点，每相邻两计数点间还有4个点（图中未标出），计数点间的距离如图2所示．已知m1=80g、m2=120g，则（g取9.8m/s2，所有结果均保留三位有效数字）
