题目内容
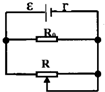 如图所示电路,电源电动势为4V,内电阻为1Ω,R0为定值电阻,值为3Ω,变阻器的最大阻值为20Ω.
如图所示电路,电源电动势为4V,内电阻为1Ω,R0为定值电阻,值为3Ω,变阻器的最大阻值为20Ω.(1)当变阻器阻值调至R1=
(2)当变阻器阻值调至某一适当值时,变阻器上消耗的功率最大,该最大功率为
分析:1、从电源的角度看功率,当内阻与外阻阻值相等时电源输出功率最大.
2、设当变阻器阻值为Rx时,变阻器上消耗的功率最大,此时变阻器中的电流为Ix.运用闭合电路的欧姆定律解出Ix和Rx的关系,即用Rx表示Ix,则变阻器上消耗的功率为Px=Ix2Rx,代入数据得到Rx的二次函数,根据二次函数求极值的方法,讨论变阻器上消耗的最大功率.
2、设当变阻器阻值为Rx时,变阻器上消耗的功率最大,此时变阻器中的电流为Ix.运用闭合电路的欧姆定律解出Ix和Rx的关系,即用Rx表示Ix,则变阻器上消耗的功率为Px=Ix2Rx,代入数据得到Rx的二次函数,根据二次函数求极值的方法,讨论变阻器上消耗的最大功率.
解答:解:(1)当内阻与外阻阻值相等时电源输出功率最大,
所以r=R=
代入数据1=
解得:R1=1.5Ω.
(2)设当变阻器阻值为Rx时,变阻器上消耗的功率最大,此时变阻器中的电流为Ix,
根据闭合电路的欧姆定律有IxRx+(Ix+
)r=E
所以
=
代入数据
=
得Ix=
则变阻器上消耗的功率为
Px=Ix2Rx=(
)2Rx=
Rx=
根据数学知识有
+16Rx≥2×
,即
+16Rx≥24,
所以Px≤
=3W
即变阻器上消耗的最大功率为3W.
故答案为:1.5,3.
所以r=R=
| R0R1 |
| R0+R1 |
代入数据1=
| 3R1 |
| 3+R1 |
解得:R1=1.5Ω.
(2)设当变阻器阻值为Rx时,变阻器上消耗的功率最大,此时变阻器中的电流为Ix,
根据闭合电路的欧姆定律有IxRx+(Ix+
| IxRx |
| R0 |
所以
| (R0+r)Rx+R0 |
| R0 |
| E |
| Ix |
代入数据
| 4Rx+3 |
| 3 |
| 4 |
| Ix |
得Ix=
| 12 |
| 3+4Rx |
则变阻器上消耗的功率为
Px=Ix2Rx=(
| 12 |
| 3+4Rx |
| 144 |
| 9+24Rx+16Rx2 |
| 144 | ||
|
根据数学知识有
| 9 |
| Rx |
| 9×16 |
| 9 |
| Rx |
所以Px≤
| 144 |
| 24+24 |
即变阻器上消耗的最大功率为3W.
故答案为:1.5,3.
点评:本题要求知道,当外阻等于内阻时,电源的输出功率要达到最大.
当电阻和电流都变化时,此时用电阻表示电流,再计算功率,根据二次函数讨论极值.此题有一定的难度,是一道好题.
当电阻和电流都变化时,此时用电阻表示电流,再计算功率,根据二次函数讨论极值.此题有一定的难度,是一道好题.

练习册系列答案
相关题目
 如图所示电路,电源电压不变,已知:电阻R1的电阻值为1Ω,电阻R2的阻值为3Ω,则电流表 1 和电流表 2 的示数比为( )
如图所示电路,电源电压不变,已知:电阻R1的电阻值为1Ω,电阻R2的阻值为3Ω,则电流表 1 和电流表 2 的示数比为( ) 如图所示电路,电源电动势为E,内阻为r,Rt为光敏电阻(光照强度增加时,其电阻值减小).现增加光照强度,则下列判断正确的是( )
如图所示电路,电源电动势为E,内阻为r,Rt为光敏电阻(光照强度增加时,其电阻值减小).现增加光照强度,则下列判断正确的是( ) 如图所示电路,电源电动势E=12.0V,内电阻r=2.0Ω,R1=40Ω,R2=20Ω,R3=12Ω,R4=10Ω.电压表和电流表都是理想电表.图中两电表示数各是多大?
如图所示电路,电源电动势E=12.0V,内电阻r=2.0Ω,R1=40Ω,R2=20Ω,R3=12Ω,R4=10Ω.电压表和电流表都是理想电表.图中两电表示数各是多大?
