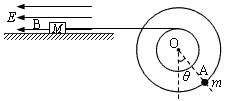
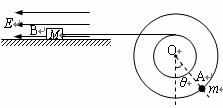
题目内容
半径分别为r=0.1m和R=2r=0.2m的两个质量不计的圆盘,共轴固定连接在一起,可以绕水平轴O无摩擦转动,大圆盘的边缘上固定有一个可看作质点的质量m=0.1kg的小球A,小圆盘上绕有细线,细线的另一端与放在光滑绝缘水平桌面上的带电小物块B水平相连,物块B的质量M=0.12kg,带电量为q=1.0×10-4C,处于水平向左的匀强电场中,电场强度大小为E=104N/C.整个系统在如图所示位置处于静止平衡状态,此时OA连线与竖直方向的夹角为θ.求:(1)夹角θ的大小.
(2)缓慢顺时针转动圆盘,使小球A位于转轴O的正下方由静止释放,当圆盘转过45°角时物块B运动的速度多大?
(3)缓慢顺时针转动圆盘,使小球A重新回到转轴O的正下方,改变电场强度大小使其为E后由静止释放系统,物块B向左运动的最大距离s=
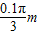 ,则电场强度E多大?
,则电场强度E多大?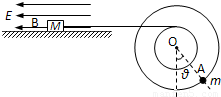
【答案】分析:(1)对圆盘研究,受到细线的拉力和物块B的重力,由力矩平衡条件列方程求解.
(2)对系统研究,小球A位于转轴O的正下方由静止释放后,拉力做正功,物块重力做负功,根据动能定理求出物块B运动的速度.
(3)物块B向左运动的最大距离s=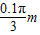 ,确定圆盘转过的最大角度,再运用动能定理求解.
,确定圆盘转过的最大角度,再运用动能定理求解.
解答: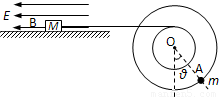 解:(1)对物块B:T=qE=1.0×10-4×104N=1.0N
解:(1)对物块B:T=qE=1.0×10-4×104N=1.0N
对圆盘,由力矩平衡T?r=mg?2rsinθ
得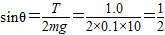 ,θ=30°
,θ=30°
(2)对整个系统,由动能定理得
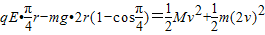
代入数据,解得v=0.28m/s
(3)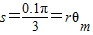 ,圆盘转过的最大角度
,圆盘转过的最大角度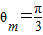
对整个系统,由动能定理qE?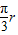 =mg?2r(1-cos
=mg?2r(1-cos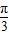 )
)
解得E=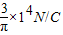 =9.55×103N/C
=9.55×103N/C
答:(1)夹角θ的大小为30°.
(2)缓慢顺时针转动圆盘,使小球A位于转轴O的正下方由静止释放,当圆盘转过45°角时物块B运动的速度为0.28m/s.
(3)缓慢顺时针转动圆盘,使小球A重新回到转轴O的正下方,改变电场强度大小使其为E后由静止释放系统,物块B向左运动的最大距离s=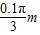 ,电场强度E为9.55×103N/C.
,电场强度E为9.55×103N/C.
点评:本题是力矩平衡与动能定理的综合应用,容易产生错误的解答是认为使小球A位于转轴O的正下方由静止释放,当圆盘转过45°角时力矩平衡.
(2)对系统研究,小球A位于转轴O的正下方由静止释放后,拉力做正功,物块重力做负功,根据动能定理求出物块B运动的速度.
(3)物块B向左运动的最大距离s=
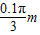 ,确定圆盘转过的最大角度,再运用动能定理求解.
,确定圆盘转过的最大角度,再运用动能定理求解.解答:
 解:(1)对物块B:T=qE=1.0×10-4×104N=1.0N
解:(1)对物块B:T=qE=1.0×10-4×104N=1.0N对圆盘,由力矩平衡T?r=mg?2rsinθ
得
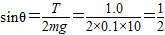 ,θ=30°
,θ=30°(2)对整个系统,由动能定理得
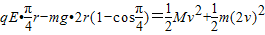
代入数据,解得v=0.28m/s
(3)
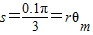 ,圆盘转过的最大角度
,圆盘转过的最大角度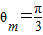
对整个系统,由动能定理qE?
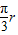 =mg?2r(1-cos
=mg?2r(1-cos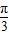 )
)解得E=
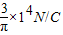 =9.55×103N/C
=9.55×103N/C答:(1)夹角θ的大小为30°.
(2)缓慢顺时针转动圆盘,使小球A位于转轴O的正下方由静止释放,当圆盘转过45°角时物块B运动的速度为0.28m/s.
(3)缓慢顺时针转动圆盘,使小球A重新回到转轴O的正下方,改变电场强度大小使其为E后由静止释放系统,物块B向左运动的最大距离s=
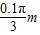 ,电场强度E为9.55×103N/C.
,电场强度E为9.55×103N/C.点评:本题是力矩平衡与动能定理的综合应用,容易产生错误的解答是认为使小球A位于转轴O的正下方由静止释放,当圆盘转过45°角时力矩平衡.

练习册系列答案
相关题目
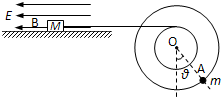 半径分别为r=0.1m和R=2r=0.2m的两个质量不计的圆盘,共轴固定连接在一起,可以绕水平轴O无摩擦转动,大圆盘的边缘上固定有一个可看作质点的质量m=0.1kg的小球A,小圆盘上绕有细线,细线的另一端与放在光滑绝缘水平桌面上的带电小物块B水平相连,物块B的质量M=0.12kg,带电量为q=1.0×10-4C,处于水平向左的匀强电场中,电场强度大小为E0=104N/C.整个系统在如图所示位置处于静止平衡状态,此时OA连线与竖直方向的夹角为θ.求:
半径分别为r=0.1m和R=2r=0.2m的两个质量不计的圆盘,共轴固定连接在一起,可以绕水平轴O无摩擦转动,大圆盘的边缘上固定有一个可看作质点的质量m=0.1kg的小球A,小圆盘上绕有细线,细线的另一端与放在光滑绝缘水平桌面上的带电小物块B水平相连,物块B的质量M=0.12kg,带电量为q=1.0×10-4C,处于水平向左的匀强电场中,电场强度大小为E0=104N/C.整个系统在如图所示位置处于静止平衡状态,此时OA连线与竖直方向的夹角为θ.求:
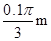 ,则电场强度E多大?
,则电场强度E多大?
 ,则电场强度E多大?
,则电场强度E多大?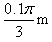 ,则电场强度E多大?
,则电场强度E多大?