题目内容
(9分)如图所示,M是一块平面镜,位于透明液体中,镜面水平向上放置,镜面到液面的距离h=0.8 m.一束细光线竖直向下射来,通过液体射到平面镜上.现将平面镜以入射点为水平轴顺时针转过18.5°角,转到图中虚线所示的位置,光线经平面镜反射后,在液面处分成两束,且这两束光恰好垂直.(已知sin 37°=0.6,设平面镜较短,光线在平面镜上只发生一次反射)求:
①光从开始进入液面到第一次离开液面的时间;
②平面镜绕水平轴顺时针至少转过多少度,才能没有光线从液面射出.
①8×10-9 s②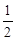 acrsin
acrsin .
.
解析试题分析:①依题意作出的光路图如图所示,当镜面转过18.5°角时,反射光线转过37°角,即
∠AOO′=∠OO′N′=37°由几何知识可得∠CO′N=53°
则液体的折射率n=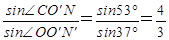
光在液体中的路程为s=h+ =1.8 m
=1.8 m
光从开始进入液面到第一次离开液面的时间t=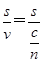 =8×10-9 s
=8×10-9 s
②光在液面发生全反射的临界角sinC=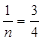
则当∠AOO′=∠OO′N′=C时,光在液面刚好发生全反射,没有光线从液面射出,此时平面镜绕水平轴顺时针转过的最小角度为α= =
=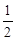 acrsin
acrsin .
.
考点:考查了光的折射与全反射

练习册系列答案
相关题目
如图所示,由导热气缸和活塞封闭有一定质量的理想气体,活塞和气缸壁之间摩擦不计。已知大气压强 ,活塞面积
,活塞面积 ,活塞质量m=4kg。环境温度不变,今在活塞上方逐渐加入细砂,使活塞缓慢下降,直到活塞距离底部的高度为初始的2/3。
,活塞质量m=4kg。环境温度不变,今在活塞上方逐渐加入细砂,使活塞缓慢下降,直到活塞距离底部的高度为初始的2/3。
(g取 )
)
①上述过程中下列说法正确的是
| A.缸内气体的内能一定增加 |
| B.缸内气体的压强一定增加 |
| C.单位时间内气体分子对活塞的碰撞次数不变 |
| D.缸内气体将吸收热量 |
下列关于光学现象的说法中正确的是
| A.用光导纤维束传送图像信息,这是光的衍射的应用 |
| B.太阳光通过三棱镜形成彩色光谱,这是光的干涉的结果 |
| C.在照相机镜头前加装偏振滤光片拍摄日落时的景物,可使景象更清晰 |
| D.透过平行于日光灯的窄缝观察正常发光的日光灯时能看到彩色条纹,这是光的色散现象 |





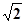 的玻璃柱体,其横截面是圆心角为90°。半径为R的扇形NBC。该柱体厚度为h,即MN=DC=AB=h。一束刚好覆盖ABNM面的单色光,以与该面成450角的方向照射到ABNM面上。若只考虑首次入射到ABCD面上的光,则ABCD面上有光透出部分的面积为( )
的玻璃柱体,其横截面是圆心角为90°。半径为R的扇形NBC。该柱体厚度为h,即MN=DC=AB=h。一束刚好覆盖ABNM面的单色光,以与该面成450角的方向照射到ABNM面上。若只考虑首次入射到ABCD面上的光,则ABCD面上有光透出部分的面积为( ) 
 B.
B.  C.
C.  D.
D. 
