题目内容
一辆实验小车可沿水平地面(图中标有左右的直线)上的长直轨道匀速向右运动.有一台发出细光束的激光器装在小转台M上,到轨道的距离为d="10" m,如图所示,转台匀速转动,使激光束在水平面内扫描,扫描一周的时间为T="60" s,光束转动方向如图中箭头所示,当光束与MN的夹角为45°时,光束正好射到小车上,如果再经过Δt="2.5" s光束又射到小车上,则小车的速度为多少?


(1) v1="1.7" m/s(2) 当光束照射小车时,小车正远离N点,这时小车的速度应为2.9 m/s.
本题考查光的直线传播和匀速圆周运动规律,是一道设计新颖的好题,要求学生画出小车运动位置的示意图,才能求出符合题意的两个结果.在Δt内光束转过角度为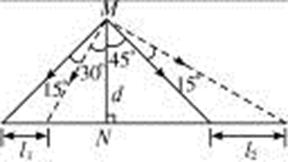
 (①式),如图所示,有两种可能:
(①式),如图所示,有两种可能:
(1)光束照射小车时,小车正在接近N点,Δt内光束与MN的夹角从45°变为30°,小车走过l1,速度应为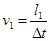 (②式);由图可知
(②式);由图可知
l1=d(tan45°-tan30°)(③式)
由②③两式并代入数值,得v1="1.7" m/s(④式).
(2)光束照射小车时,小车正在远离N点,Δt内光束与MN的夹角从45°变为60°,小车走过l2,速度应为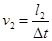 (⑤式)
(⑤式)
由图可知l2=d(tan60°-tan45°)(⑥式)
由⑤⑥两式并代入数值,得v2="2.9" m/s.
答案:(1)当光束照射小车时,小车正在接近N点,这时小车的速度应为1.7 m/s;(2)当光束照射小车时,小车正远离N点,这时小车的速度应为2.9 m/s

 (①式),如图所示,有两种可能:
(①式),如图所示,有两种可能:(1)光束照射小车时,小车正在接近N点,Δt内光束与MN的夹角从45°变为30°,小车走过l1,速度应为
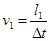 (②式);由图可知
(②式);由图可知l1=d(tan45°-tan30°)(③式)
由②③两式并代入数值,得v1="1.7" m/s(④式).
(2)光束照射小车时,小车正在远离N点,Δt内光束与MN的夹角从45°变为60°,小车走过l2,速度应为
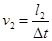 (⑤式)
(⑤式)由图可知l2=d(tan60°-tan45°)(⑥式)
由⑤⑥两式并代入数值,得v2="2.9" m/s.
答案:(1)当光束照射小车时,小车正在接近N点,这时小车的速度应为1.7 m/s;(2)当光束照射小车时,小车正远离N点,这时小车的速度应为2.9 m/s

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
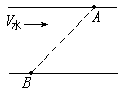


 ,河水流速为
,河水流速为 ,则当小船的船头指向河对岸开动时,从地面上看小船的速度为()
,则当小船的船头指向河对岸开动时,从地面上看小船的速度为()

