题目内容
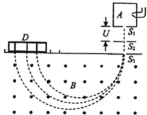
【题目】如图所示,光滑绝缘曲面与水平传送带固定在一竖直平面内,且在B处平滑连接,整个装置处在竖直向下的匀强电场中.水平传送带长为L=10m,且以v=5m/s的恒定速度匀速逆时针方向转动.一质量为m=0.2kg,电荷量为q=0.2C的带电的小物体从距传送带某一高度的A点由静止滑下,滑过B点后经时t=2s恰好运动到传送带最后端C处,不考虑滑块与传送带摩擦时的电量损失,已知小物体与传送带之间的动摩擦因数为μ=0.25,取g=10m/s2,求:
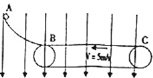
(1)匀强电场的电场强度E;
(2)小物体再次经过B点后滑上曲面时离传送带的最大竖直高度;
(3)从小物体滑上传送带到再次经过B点的过程中,小物体与传送带间因摩擦而产生的热量.
【答案】(1)E=10N/C (2)h=0.625m (3)Q=22.5J
【解析】
(1)小物块向左做匀减速直线运动,结合位移时间公式求出匀减速运动的加速度大小,根据牛顿第二定律求出匀强电场的电场强度.
(2)再次返回时,先做匀加速运动,根据牛顿第二定律求出加速度,结合速度时间公式求出速度达到传送带速度所需的时间,以及求出此时的位移,判断出小物块在传送带上的运动规律,得出到达B点的速度,再根据动能定理求出滑上曲面后离传送带的最大竖直高度.
(3)根据运动学公式求出小物块在传送带上运动的相对路程,从而得出因摩擦产生的热量.
(1)设小物体向左匀减速运动的加速度为a,则有:![]()
代入数据解得:a=5m/s2,
由牛顿第二定律有:μ(qE+mg)=ma,
代入数据解得:E=10N/C.
(2)小物体从C返回的过程中,加速度为a′,则有:μ(qE+mg)=ma′,
代入数据解得:a′=5m/s2.
达到与传送带共同速度所需的时间为t′,则有:v=a′t′
解得t′=1s.
物块的位移为:![]()
则小物块向右经过B点的速度为:v=5m/s,
由动能定理得:![]()
代入数据解得:h=0.625m
(3)小物块向左运动的过程中,相对位移为:△x1=L+vt=20m
小物体向右运动的过程中,相对位移为:△x2=vt′-x=2.5m
则全程产生的热量为:Q=μ(qE+mg)(△x1+△x2)=22.5J

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案