题目内容
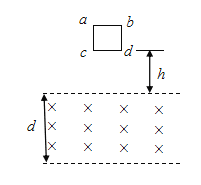
【题目】如图所示，相距为d的两条水平虚线之间是方向水平向里的匀强磁场，磁感应强度为B，正方形线圈abcd边长为L（L<d），质量为m、电阻为R，将线圈在磁场上方h高处由静止释放，cd边刚进入磁场时速度为v0，cd边刚离开磁场时速度也为v0，则线圈穿过磁场的过程中（从cd边刚进入磁场起一直到ab边离开磁场为止）
A. 感应电流所做的功为mgd
B. 感应电流所做的功为mg（d－L）
C. 线圈的最小速度一定是2
D. 线圈的最小速度可能为mgR/B2L2
【答案】D
【解析】试题分析：根据能量守恒，研究从cd边刚进入磁场到cd边刚穿出磁场的过程：动能变化量为0，重力势能转化为线框进入磁场的过程中产生的热量，Q=mgd．cd边刚进入磁场时速度为v0，cd边刚离开磁场时速度也为v0，所以从cd边刚穿出磁场到ab边离开磁场的过程，线框产生的热量与从cd边刚进入磁场到ab边刚进入磁场的过程产生的热量相等，所以线圈从cd边进入磁场到ab边离开磁场的过程，产生的热量Q′=2mgd，感应电流做的功为2mgd．故AB错误．因为进磁场时要减速，线圈全部进入磁场后做匀加速运动，则知线圈刚全部进入磁场的瞬间速度最小．设线圈的最小速度为vm．线圈从开始下落到线圈刚完全进入磁场的过程，根据能量守恒定律得：mg（h+L）=Q+
mvm2，由上可知，Q="mgd," 解得线圈的最小速度为：
．故C错误．线框可能先做减速运动，在完全进入磁场前已做匀速运动，刚完全进入磁场时的速度最小，则
，则最小速度
．故D正确．故选D．
练习册系列答案
相关题目
