题目内容
【题目】如图所示，在斜面上O点先后以v0和2v0的速度水平抛出A、B两小球，则从抛出至第一次着地，两小球的水平位移大小之比可能为（ ）
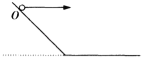
A. 1：2 B. 1：3 C. 1：4 D. 1：5
【答案】ABC
【解析】试题分析：抛出的小球做平抛运动，分都落在斜面上，一个在斜面上一个在水平面上，和两个都落在水平面来计算．
解：当A、B两个小球都能落到水平面上时，由于两者的下落高度相同，运动的时间相同，则水平位移之比为初速度之比，为1：2，所以A正确；
当A、B都落在斜面的时候，它们的竖直位移和水平位移的比值即为斜面夹角的正切值，
即
=tanθ，
整理可得，时间t=
，
两次平抛的初速度分别为υ0和2υ0，
所以运动的时间之比为
=
=
．
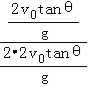两小球的水平位移大小之比为xA：xB=v0tA：2v0tB=1：4，所以C正确．
当只有A落在斜面上的时候，A、B水平位移之比在1：4和1：2之间，所以B正确．
故选ABC．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
