题目内容
7.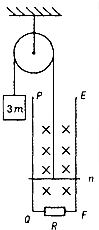 在如图所示的裝置中,悬挂在某固定点的光滑定滑轮上绕有柔软细线.细线的一端系一质量为m、电阻为r的金属杆,另一端系一质量为3m的重物.在竖直平面内有间距为L的足够长的平行金属导軌PQ、EF,在QF之间连接有阻值为R的电阻.其余电阻不计,磁感应强度为B0的匀强磁场与导轨平面垂直,开始时金属杆置于导轨下端QF处,将重物由静止释放,当重物下降h时恰好达到稳定速度而匀速下降.运动过程中金属杆始终与导轨垂直且接触良好.忽略所有摩擦,重力加速度为g,求:
在如图所示的裝置中,悬挂在某固定点的光滑定滑轮上绕有柔软细线.细线的一端系一质量为m、电阻为r的金属杆,另一端系一质量为3m的重物.在竖直平面内有间距为L的足够长的平行金属导軌PQ、EF,在QF之间连接有阻值为R的电阻.其余电阻不计,磁感应强度为B0的匀强磁场与导轨平面垂直,开始时金属杆置于导轨下端QF处,将重物由静止释放,当重物下降h时恰好达到稳定速度而匀速下降.运动过程中金属杆始终与导轨垂直且接触良好.忽略所有摩擦,重力加速度为g,求:(1)电阻R中的感应电流方向;
(2)重物匀速下降的速度v;
(3)重物从释放到下降h的过程中,电阻R中产生的焦耳热QR:
(4)若将重物下降h时刻记作t=0,速度记为v0,从此时刻起,磁感应强度逐渐减小,若此后金属杆中恰好不产生感应电流,則磁感应强度B怎样随时间t变化(写出B与t的关系式)
分析 (1)由右手定则判断出感应电流方向,判断出R中的电流方向.
(2)重物匀速下降时,金属杆匀速上升,受力平衡.推导出安培力,由平衡条件列式求出速度v.
(3)重物从释放到下降h的过程中,重物的重力势能减小转化为杆的重力势能和动能、重物的动能及整个回路的内能,根据能量守恒求出整个回路产生的焦耳热,根据串联电路电流关系,求出电阻R中产生的焦耳热QR;
(4)当回路中总磁通量不变时,金属棒中不产生感应电流,此时棒将导轨做匀加速运动.根据磁通量不变,列式求B与t的关系式.
解答 解:(1)释放重物后,金属杆向上运动,由右手定则可知,电阻R中的感应电流方向为Q→R→F;
(2)重物匀速下降时,金属棒匀速上升,处于平衡状态,
对金属棒,由平衡条件得:T=mg+F,
金属棒受到的安培力:F=B0IL=$\frac{{B}_{0}^{2}{L}^{2}v}{R+r}$,
对重物,由平衡条件得:T=3mg,
解得:v=$\frac{2mg(R+r)}{{B}_{0}^{2}{L}^{2}}$;
(3)设电路中产生的总焦耳热为Q,由能量守恒定律得:
3mgh-mgh=$\frac{1}{2}$•(3m)v2+$\frac{1}{2}$mv2+Q,
电阻R中产生的焦耳热:QR=$\frac{R}{R+r}$Q,
解得:QR=$\frac{2mghR}{R+r}$-$\frac{8{m}^{3}{g}^{2}(R+r)R}{{B}_{0}^{4}{L}^{4}}$;
(4)金属杆中恰好不产生感应电流,即磁通量不变:Φ0=Φt,
hLB0=(h+h2)LBt,
h2=$\frac{1}{2}$at2,
又 a=$\frac{3mg-mg}{3m+m}=\frac{1}{2}g$
解得,磁感应强度B怎样随时间t变化关系:Bt=$\frac{{B}_{0}h}{h+{v}_{0}t+\frac{g}{4}{t}^{2}}$;
答:(1)电阻R中的感应电流方向为:Q→R→F;
(2)重物匀速下降的速度为$\frac{2mg(R+r)}{{B}_{0}^{2}{L}^{2}}$;
(3)重物从释放到下降h的过程中,电阻R中产生的焦耳热为$\frac{2mghR}{R+r}$-$\frac{8{m}^{3}{g}^{2}(R+r)R}{{B}_{0}^{4}{L}^{4}}$;
(4)磁感应强度B随时间t的变化关系为Bt=$\frac{{B}_{0}h}{h+{v}_{0}t+\frac{g}{4}{t}^{2}}$.
点评 本题分别从力和能量两个角度研究电磁感应现象,关键是计算安培力和分析能量如何变化,以及把握没有感应电流产生的条件.

 甲、乙两汽车在同一平直公路上行驶,其速度-时间图象如图所示.已知两汽车在第25s末到达同一位置,则甲、乙两汽车( )
甲、乙两汽车在同一平直公路上行驶,其速度-时间图象如图所示.已知两汽车在第25s末到达同一位置,则甲、乙两汽车( )| A. | 运动的加速度之比为1:4 | |
| B. | 运动的加速度之比为1:3 | |
| C. | 到达同一位置前相距最远距离为180m | |
| D. | 到达同一位置前相距最远距离为400m |
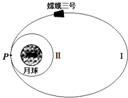 如图所示是嫦娥三号奔月过程中某阶段的运动示意图,嫦娥三号沿椭圆轨道Ⅰ运动到近月点P处变轨进入圆轨道Ⅱ,嫦娥三号在圆轨道Ⅱ做圆周运动的轨道半径为r,周期为T,已知引力常量为G,下列说法中正确的是( )
如图所示是嫦娥三号奔月过程中某阶段的运动示意图,嫦娥三号沿椭圆轨道Ⅰ运动到近月点P处变轨进入圆轨道Ⅱ,嫦娥三号在圆轨道Ⅱ做圆周运动的轨道半径为r,周期为T,已知引力常量为G,下列说法中正确的是( )| A. | 由题中(含图中)信息可求得月球的质量 | |
| B. | 由题中(含图中)信息可求得月球第一宇宙速度 | |
| C. | 嫦娥三号在P处变轨时必须点火加速 | |
| D. | 嫦娥三号沿椭圆轨道Ⅰ运动到P处时的加速度大于沿圆轨道Ⅱ运动到P处时的加速度 |
 如图所示,有一矩形线圈的面积为S,匝数为N,内阻不计,绕OO′轴在磁感应强度为B的水平方向匀强磁场中以角速度ω做匀速转动,从图示位置开始计时.矩形线圈通过滑环接一理想变压器,滑动接头P上下移动时可改变输出电压,副线圈接有可调电阻R,下列判断正确的是( )
如图所示,有一矩形线圈的面积为S,匝数为N,内阻不计,绕OO′轴在磁感应强度为B的水平方向匀强磁场中以角速度ω做匀速转动,从图示位置开始计时.矩形线圈通过滑环接一理想变压器,滑动接头P上下移动时可改变输出电压,副线圈接有可调电阻R,下列判断正确的是( )| A. | 矩形线圈产生的感应电动势的瞬时值表达式为e=NBSωsinωt | |
| B. | 矩形线圈从图示位置经过$\frac{π}{2ω}$时间内,通过电流表的电荷量为零 | |
| C. | 当P位置不动R增大时,电压表读数也增大 | |
| D. | 当P位置向上移动、R不变时,电流表读数增大 |
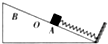 如图所示,一轻弹簧一端与挡板固定,另一端自由伸长时位于O点,当另一端和物块相连时,A、B是物块能保持静止的位置中离挡板最近和最远的点.A、B两点离挡板的距离分别为x1、x2.物块与斜面的最大静摩擦力为f,则弹簧的劲度系数为( )
如图所示,一轻弹簧一端与挡板固定,另一端自由伸长时位于O点,当另一端和物块相连时,A、B是物块能保持静止的位置中离挡板最近和最远的点.A、B两点离挡板的距离分别为x1、x2.物块与斜面的最大静摩擦力为f,则弹簧的劲度系数为( )| A. | $\frac{f}{{x}_{2}+{x}_{1}}$ | B. | $\frac{2f}{{x}_{2}+{x}_{1}}$ | C. | $\frac{f}{{x}_{2}-{x}_{1}}$ | D. | $\frac{2f}{{x}_{2}-{x}_{1}}$ |
| A. | 电磁波在真空中传播时,每处的电场强度方向和磁感应强度方向总是平行的 | |
| B. | 拍摄玻璃橱窗内的物品时,在镜头前加装一个偏振片是为了增加透射光的强度 | |
| C. | 站在地面上的人观察一根沿自身长度方向以接近光速运动的杆,观察到的长度比杆静止时的短 | |
| D. | 某同学在“用单摆测重力加速度”的实验中,测摆长时漏加了小球的半径,则测得的重力加速度值偏大 |
| A. | 电荷放在电势越高的地方,其电势能就越大 | |
| B. | 无论正电荷还是负电荷,只要它克服电场力做功,它的电势能都增大 | |
| C. | 正电荷在电场中某点的电势能,一定大于等量负电荷在该点具有的电势能 |
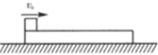 如图所示,质量M=8.0kg、长L=2.0m的木板静置在水平地面上,质量m=0.50kg的小滑块(可视为质点)以速度v0=3.0m/s从木板的左端冲上木板.已知滑块与木板间的动摩擦因数μ=0.20,重力加速度g取10m/s2.
如图所示,质量M=8.0kg、长L=2.0m的木板静置在水平地面上,质量m=0.50kg的小滑块(可视为质点)以速度v0=3.0m/s从木板的左端冲上木板.已知滑块与木板间的动摩擦因数μ=0.20,重力加速度g取10m/s2.