题目内容
 一个底面粗糙,质量为m的劈放在水平面上,劈的斜面光滑且倾角为30°,如图所示.现用一端固定的轻绳系一质量也为m的小球.绳与斜面夹角为30°,求:
一个底面粗糙,质量为m的劈放在水平面上,劈的斜面光滑且倾角为30°,如图所示.现用一端固定的轻绳系一质量也为m的小球.绳与斜面夹角为30°,求:(1)当劈静止时绳子拉力为多大?
(2)若地面对劈的最大静摩擦力等于地面对劈的支持力的K倍,为使整个系统静止,K值必须满足什么条件?
分析:小球和斜面均处于平衡状态,分别对小球和斜面受力分析应用合成或分解即可解决.
解答:解:(1)选小球为研究对象,受力分析并合成如图:

由平衡条件:F′=mg
由平面几何知识可得:N与F′夹角为30°,T与F′夹角也为30°
故画出的平行四边形为菱形,连接对角线便可找出直角三角形:
由:cos30°=
得:T=
mg
(2)选小球和斜面组成的系统为研究对象,受力分析如图:
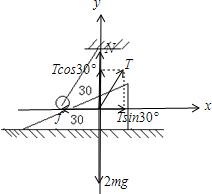
由平衡条件得:
N+Tcos30°=2mg,解得:N=
mg
f=Tsin30°,解得:f=
mg
fMAX=KN=K
mg
为使整个系统静止,f≤fMAX
mg≤K
mg
解得:K≥
答:(1)当劈静止时绳子拉力为T=
mg.
(2)若地面对劈的最大静摩擦力等于地面对劈的支持力的K倍,为使整个系统静止,K值必须满足K≥
.

由平衡条件:F′=mg
由平面几何知识可得:N与F′夹角为30°,T与F′夹角也为30°
故画出的平行四边形为菱形,连接对角线便可找出直角三角形:
由:cos30°=
| ||
| T |
| ||
| 3 |
(2)选小球和斜面组成的系统为研究对象,受力分析如图:

由平衡条件得:
N+Tcos30°=2mg,解得:N=
| 3 |
| 2 |
f=Tsin30°,解得:f=
| ||
| 6 |
fMAX=KN=K
| 3 |
| 2 |
为使整个系统静止,f≤fMAX
| ||
| 6 |
| 3 |
| 2 |
解得:K≥
| ||
| 9 |
答:(1)当劈静止时绳子拉力为T=
| ||
| 3 |
(2)若地面对劈的最大静摩擦力等于地面对劈的支持力的K倍,为使整个系统静止,K值必须满足K≥
| ||
| 9 |
点评:对小球和斜面进行受力分析,运用力的合成或分解结合共点力平衡条件解决问题.选择好合适的研究对象有事半功倍的效果.

练习册系列答案
相关题目
 一个底面粗糙、质量为M=5kg的劈放在粗糙的水平面上,劈的斜面光滑且与水平面成30°角;现用一端固定的轻绳系一质量为m=3kg的小球,小球放在斜面上,小球静止时轻绳与竖直方向的夹角也为30°,如图所示,( g=10m/s2)试求:
一个底面粗糙、质量为M=5kg的劈放在粗糙的水平面上,劈的斜面光滑且与水平面成30°角;现用一端固定的轻绳系一质量为m=3kg的小球,小球放在斜面上,小球静止时轻绳与竖直方向的夹角也为30°,如图所示,( g=10m/s2)试求: 如图所示,一个底面粗糙,质量为m的斜面体静止在水平地面上,斜面体斜面是光滑的,倾角为30°.现用一端固定的轻绳系一质量也为m的小球,小球静止时轻绳与斜面的夹角也是30°.求地面与斜面间的动摩擦因数至少多大?(设最大静摩擦力大小等于滑动摩擦力大小)
如图所示,一个底面粗糙,质量为m的斜面体静止在水平地面上,斜面体斜面是光滑的,倾角为30°.现用一端固定的轻绳系一质量也为m的小球,小球静止时轻绳与斜面的夹角也是30°.求地面与斜面间的动摩擦因数至少多大?(设最大静摩擦力大小等于滑动摩擦力大小)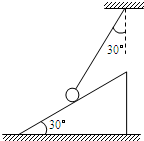 一个底面粗糙,质量为m的劈放在粗糙水平面上,劈的斜面光滑且与水平面夹角为30°,现用一端固定的轻绳系一质量也为m的小球,小球与斜面的夹角为30°,如图所示.
一个底面粗糙,质量为m的劈放在粗糙水平面上,劈的斜面光滑且与水平面夹角为30°,现用一端固定的轻绳系一质量也为m的小球,小球与斜面的夹角为30°,如图所示.