题目内容
14.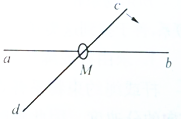 如图所示,纸面内两根足够长的细杆ab,cd都穿过小环M,杆ab两端固定,杆CD可以在纸面内绕过d点并与纸面垂直的定轴转动,若杆cd从图示位置开始,按照图中箭头所示的方向,以匀角速度转动,则小环M的加速度( )
如图所示,纸面内两根足够长的细杆ab,cd都穿过小环M,杆ab两端固定,杆CD可以在纸面内绕过d点并与纸面垂直的定轴转动,若杆cd从图示位置开始,按照图中箭头所示的方向,以匀角速度转动,则小环M的加速度( )| A. | 逐渐增大 | B. | 逐渐减小 | C. | 先增加后减小 | D. | 先减小后增加 |
分析 根据圆周运动规律可得出M点的转动线速度,再由运动的合成和分析求出其合速度;则由求导可求得加速度的表达式.
解答 解:设cd与竖直方向夹角为θ,则有:θ=ωt;
d到ab竖直距离h,则环M的速度v=$\frac{ωr}{cosθ}$=$\frac{ωh}{co{s}^{2}θ}$=$\frac{ωh}{co{s}^{2}ωt}$
则环M的加速度a等于v的导数;
即a=v′=-2ωhcos-3ωt(-sinωt)ω=$\frac{{ω}^{2}hsinωt}{co{s}^{3}ωt}$;
故说明加速度越来越大;
故选:A.
点评 本题考查运动的合成与分解的应用;要注意明确环沿杆的运动速度是合速度,而杆的转动线速度为分速度.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4.下列说法正确的是( )
| A. | 随着科技的发展,永动机是可以制成的 | |
| B. | 太阳照到地球上的光能转化成了其他形式的能力,但照射到宇宙其他空间的能量都消失了 | |
| C. | “既要马儿跑,又让马儿不吃草”违背了能量守恒定律,因而是不可能的 | |
| D. | 有种“全自动”手表,不用上发条也不用任何形式的能源,却能一直走动,说明能量可以凭空产生的 |
9.以下是有关近代物理内容的若干叙述,其中正确的有( )
| A. | 有10个放射性元素的原子核,当有5个原子核发生衰变所需的时间就是该放射性元素的半衰期 | |
| B. | 用α粒子轰击铍核(${\;}_{4}^{9}$Be),可以得到碳核(${\;}_{6}^{12}$C)和质子 | |
| C. | 氢原子的核外电子由较高能级迁到较低能级时,要释放一定频率的光子,同时电子的动能增大,电势能减小 | |
| D. | 用γ射线治疗肿瘤时一定要严格控制剂量,以免对人体正常组织造成太大的伤害 |
3.下列说法中正确的是( )
| A. | 甲物体受乙物体的作用,则乙物体一定同时受到甲物体的作用 | |
| B. | 甲物体对乙物体的作用一定是作用力,而乙物体对甲物体的作用一定是反作用力 | |
| C. | 若把甲、乙两物体看成质点,则甲、乙两物体间的作用力和反作用力一定在甲、乙两物体的连线上 | |
| D. | 若甲物体对乙物体的作用力竖直向上,则乙物体对甲物体的作用力也一定竖直向上 |
10. 如图所示,在竖直平面内的固定光滑元轨道的最高点有一个光滑的小孔,质量为m的小环套在圆轨道上,用细线通过小孔系在环上,缓慢 拉动细线,使环沿轨道上移,在移动过程中拉力F和轨道对小环的作用力FN的大小变化情况是( )
如图所示,在竖直平面内的固定光滑元轨道的最高点有一个光滑的小孔,质量为m的小环套在圆轨道上,用细线通过小孔系在环上,缓慢 拉动细线,使环沿轨道上移,在移动过程中拉力F和轨道对小环的作用力FN的大小变化情况是( )
 如图所示,在竖直平面内的固定光滑元轨道的最高点有一个光滑的小孔,质量为m的小环套在圆轨道上,用细线通过小孔系在环上,缓慢 拉动细线,使环沿轨道上移,在移动过程中拉力F和轨道对小环的作用力FN的大小变化情况是( )
如图所示,在竖直平面内的固定光滑元轨道的最高点有一个光滑的小孔,质量为m的小环套在圆轨道上,用细线通过小孔系在环上,缓慢 拉动细线,使环沿轨道上移,在移动过程中拉力F和轨道对小环的作用力FN的大小变化情况是( )| A. | F不变,FN增大 | B. | F不变,FN不变 | C. | F减小,FN不变 | D. | F增大,FN增大 |
7.一小球做加速直线运动,在第1s内通过1m,在第2s内通过2m,在第3s内通过3m,在第4s内通过4m.下面有关小球的运动情况的描述中,错误的一项是( )
| A. | 小球在这4s内的平均速度是2.5m/s | |
| B. | 小球在第3s和第4s这两秒内的平均速度是3.5 m/s | |
| C. | 小球在这4s内可能做初速度为零的匀加速直线运动 | |
| D. | 小球在这4s内的加速度可能为1m/s2 |
8. 如图甲所示,在两极板a、b的对称轴线上有一静止的电子,当在a、b之间加上如图乙所示的变化电压时(开始时a板带正电),电子的运动情况是(不计重力,板间距离足够大)( )
如图甲所示,在两极板a、b的对称轴线上有一静止的电子,当在a、b之间加上如图乙所示的变化电压时(开始时a板带正电),电子的运动情况是(不计重力,板间距离足够大)( )
 如图甲所示,在两极板a、b的对称轴线上有一静止的电子,当在a、b之间加上如图乙所示的变化电压时(开始时a板带正电),电子的运动情况是(不计重力,板间距离足够大)( )
如图甲所示,在两极板a、b的对称轴线上有一静止的电子,当在a、b之间加上如图乙所示的变化电压时(开始时a板带正电),电子的运动情况是(不计重力,板间距离足够大)( )| A. | 电子先向a板运动,再返回一直向b板运动 | |
| B. | 电子在两板间做周期性往返运动,每个周期后都要向b板逐渐靠近 | |
| C. | 电子在两板间做周期性往返运动,每个周期的位移都为零 | |
| D. | 当时间是0.1秒的奇数倍时,电子偏离对称轴的距离最大 |
 如图所示,绝缘斜面上相距d=50cm的两点固定着两个绝缘的弹性挡板,斜面倾角θ=37°,斜面上方存在着平行斜面向上的匀强电场,电场强度大小为E=5.0×104N/C,现有质量m=20g、电荷量q=4×10-6C的带正电物块由斜面中点以$\sqrt{6}$m/s的速度平行斜面向下滑动,物块与弹性挡板碰撞过程不损失机械能,碰撞后以等大速度反向运动,整个过程物块所带的电荷量不变,已知物块与斜面之间的动摩擦因数为0.4,g取10m/s2,sin37°=0.6,cos37°=0.8,求物体在斜面上通过的路程.
如图所示,绝缘斜面上相距d=50cm的两点固定着两个绝缘的弹性挡板,斜面倾角θ=37°,斜面上方存在着平行斜面向上的匀强电场,电场强度大小为E=5.0×104N/C,现有质量m=20g、电荷量q=4×10-6C的带正电物块由斜面中点以$\sqrt{6}$m/s的速度平行斜面向下滑动,物块与弹性挡板碰撞过程不损失机械能,碰撞后以等大速度反向运动,整个过程物块所带的电荷量不变,已知物块与斜面之间的动摩擦因数为0.4,g取10m/s2,sin37°=0.6,cos37°=0.8,求物体在斜面上通过的路程.