Question

【题目】如图所示，质量为m的由绝缘材料制成的球与质量为M＝19m的金属球并排悬挂，摆长相同，均为l.现将绝缘球拉至与竖直方向成θ＝60°的位置自由释放，摆至最低点与金属球发生弹性碰撞．在平衡位置附近存在垂直于纸面的磁场，已知由于磁场的阻尼作用，金属球总能在下一次碰撞前停在最低点处，重力加速度为g.求：

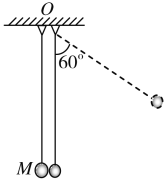
(1)第一次碰撞前绝缘球的速度v0；

(2)第一次碰撞后绝缘球的速度v1；

(3)经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于37°.

(你可能用到的数学知识：sin37°＝0.6，cos37°＝0.8,0.812＝0.656,0.813＝0.531,0.814＝0.430,0.815＝0.349,0.816＝0.282)

Answer 1

【答案】(1) ；(2) ，方向水平向右；(3)37°

【解析】(1)绝缘球下摆过程机械能守恒，由机械能守恒定律，得

mgl(1－cosθ)＝mv①

解得v0＝＝

(2)两球碰撞过程动量守恒，以绝缘球的初速度方向为正方向，

由动量守恒定律，得mv0＝mv1＋MvM②

由机械能守恒定律，得mv＝mv＋Mv③

联立②③解得

v1＝v0＝－v0＝－，负号表示方向与碰撞前方向相反，向右；

(3)设在第n次碰撞前绝缘球的速度为vn－1，碰撞后绝缘球、金属球的速度分别为vn和vN由于碰撞过程中动量守恒和机械能守恒，以碰撞前绝缘球的速度方向为正方向，

由动量守恒定律，得mvn－1＝mvn＋MvN④

由机械能守恒定律，得mv＝mv＋Mv⑤

由④、⑤两式及M＝19m，解得vn＝－vn－1

第n次碰撞后绝缘球的动能为：En＝mv＝(0.81)nE0⑥

E0为第1次碰撞前绝缘球的动能，即初始能量

得＝(0.81)n

而绝缘球在θ＝60°与θ＝37°处的势能之比为：＝0.4

根据上面数学知识：0.814＝0.430,0.815＝0.349，因此，经过5次碰撞后θ将小于37°