题目内容
如图，在平面直角坐标系xOy内，第Ⅰ象限存在沿y轴负方向的匀强电场，第Ⅳ象限以ON为直径的半圆形区域内，存在垂直于坐标平面向外的匀强磁场，磁感应强度为B．一质量为m、电荷量为q的带正电的粒子，从y轴正半轴上y=h处的M点，以速度v0垂直于y轴射入电场，经x轴上x=2h处的P点进入磁场，最后以垂直于y轴的方向射出磁场．不计粒子重力．则电场强度大小E=| mv02 |
| 2qh |
| mv02 |
| 2qh |
| 2h |
| v0 |
| 3πm |
| 4Bq |
| 2h |
| v0 |
| 3πm |
| 4Bq |
分析：在第Ⅰ象限内，粒子做类平抛运动，题干已经给出了水平位移和竖直位移，利用平抛运动的位移公式可求出电场强度的大小和在第Ⅰ象限内的运动时间．粒子进入第Ⅳ象限，在洛伦兹力的作用下做匀速圆周运动，在第Ⅰ象限中利用运动学公式可求出进入第Ⅳ的速度方向，结合几何关系，求出粒子做圆周运动的偏转角，即可求出在磁场中的运动时间．
解答：解：
粒子在第Ⅰ象限内做类平抛运动，设在第Ⅰ象限内运动的时间为t1，则：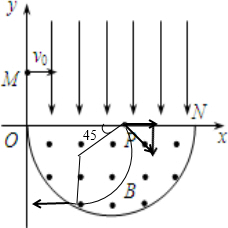
水平方向有：2h=v0t1…①
竖直方向有：h=
t12…②
①②式联立得：E=
…③
设粒子进入第Ⅳ象限时竖直方向的速度vy
则有：vy=at1=
t1…④．
①③④联立得：vy=v0
所以粒子进入第Ⅳ象限时速度与x轴的夹角为45°，粒子在第Ⅳ象限内做圆周运动的偏转角：
θ=180°-45°=135°
粒子在第Ⅳ象限内运动的时间为：
t2=
T=
…⑤
粒子从进入电场到离开磁场经历的总时间：
t=t1+t1…⑥
①⑤⑥联立得：
t=
+
故答案为：
，
+
粒子在第Ⅰ象限内做类平抛运动，设在第Ⅰ象限内运动的时间为t1，则：
水平方向有：2h=v0t1…①
竖直方向有：h=
| 1 |
| 2 |
| qE |
| m |
①②式联立得：E=
m
| ||
| 2qh |
设粒子进入第Ⅳ象限时竖直方向的速度vy
则有：vy=at1=
| qE |
| m |
①③④联立得：vy=v0
所以粒子进入第Ⅳ象限时速度与x轴的夹角为45°，粒子在第Ⅳ象限内做圆周运动的偏转角：
θ=180°-45°=135°
粒子在第Ⅳ象限内运动的时间为：
t2=
| 135° |
| 360° |
| 3πm |
| 4qB |
粒子从进入电场到离开磁场经历的总时间：
t=t1+t1…⑥
①⑤⑥联立得：
t=
| 2h |
| v0 |
| 3πm |
| 4Bq |
故答案为：
| mv02 |
| 2qh |
| 2h |
| v0 |
| 3πm |
| 4Bq |
点评：该题考查了有边界电磁场的问题，在电场中的偏转，利用平抛运动的知识求解；粒子在有边界的匀强磁场中运动，利用几何关系求解运动半径和转过的圆心角是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
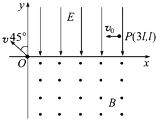如图所示，在平面直角坐标xOy内，第I象限有沿一y方向的匀强电场，第IV象限有垂直于纸面向外的匀强磁场．现有一质量为m、带电量为+q的粒子（重力不计）以初速度v0沿-x方向从坐标为（3l，l）的P点开始运动，接着进人磁场后由坐标原点O射出，射出时速度方向与y轴方向夹角为45°，求
如图所示，直角坐标平面xOy内有一条直线AC过坐标原点O与x轴成45°夹角，在OA与x轴负半轴之间的区域内存在垂直xOy平面向外的匀强磁场B，在OC与x轴正半轴之间的区域内存在垂直xOy平面向外的匀强磁场B2．现有一质量为m，带电量为q（q＞0）的带电粒子以速度v从位于直线AC上的P点，坐标为（L，L），竖直向下射出，经测量发现，此带电粒子每经过相同的时间T，会再将回到P点，已知距感应强度
