题目内容
(12分)如图所示,AB是一段位于竖直平面内的光滑轨道,高度为h,末端B处的切线方向水平.一个质量为 的小物块P从轨道顶端A处由静止释放,滑到B端后飞出,落到地面上的C点,轨迹如图中虚线BC所示.己知它落地时相对于B点的水平位移OC=
的小物块P从轨道顶端A处由静止释放,滑到B端后飞出,落到地面上的C点,轨迹如图中虚线BC所示.己知它落地时相对于B点的水平位移OC=  .现在轨道下方紧贴B点安装一水平传送带,传送带的右端与B的距离为,
.现在轨道下方紧贴B点安装一水平传送带,传送带的右端与B的距离为, /2.当传送带静止时,让P再次从A点由静止释放,它离开轨道并在传送带上滑行后从右端水平飞出,仍然落在地面的C点.当驱动轮转动从而带动传送带以速度
/2.当传送带静止时,让P再次从A点由静止释放,它离开轨道并在传送带上滑行后从右端水平飞出,仍然落在地面的C点.当驱动轮转动从而带动传送带以速度 匀速向右运动时(其它条件不变)。P的落地点为D.(不计空气阻力)
匀速向右运动时(其它条件不变)。P的落地点为D.(不计空气阻力)
(1)求P滑至B点时的速度大小:
(2)求P与传送带之间的动摩擦因数:
(3)用S-V图象表示出O、D间的距离S随速度V变化的关系。(不要求写出具体运算过程)
(12分)(1) 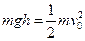 得
得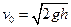 (3分)
(3分)
(2)没有传送带时,物块离开B点后做平抛运动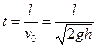 (1分)
(1分)
水平位移为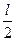 ,因此物体从传送带右端抛出的速度
,因此物体从传送带右端抛出的速度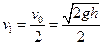 (1分)
(1分)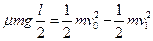 (2分)
(2分)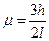 (1分)
(1分)
(3) s随速度变化的函数关系为(每段给1分,坐标1分,共4分)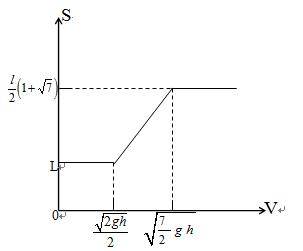
解析

练习册系列答案
相关题目
 (3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?
(3)金属棒从释放到落地过程中在电子元件上消耗的电能多大? 等效电阻
等效电阻 ,式中k为恒量。框架上有一质量为m的金属棒水平放置,金属棒与光滑框架接触良好,离地高为h,磁感应强度为B的匀强磁场与框架平面垂直。将金属棒由静止释放,棒沿框架向下运动。其它电阻不计,问:
,式中k为恒量。框架上有一质量为m的金属棒水平放置,金属棒与光滑框架接触良好,离地高为h,磁感应强度为B的匀强磁场与框架平面垂直。将金属棒由静止释放,棒沿框架向下运动。其它电阻不计,问: (3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?
(3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?

 ,S断开时,电压表示数为16V,S闭合时,电压表示数为10V,若电压表可视为理想的,则电源电动势和内电阻为多少?
,S断开时,电压表示数为16V,S闭合时,电压表示数为10V,若电压表可视为理想的,则电源电动势和内电阻为多少?