Question

如图12-6-11所示，两列简谐波均沿x轴传播，传播速度的大小相等，其中一列沿正x方向传播（图中实线所示），一列沿负x方向传播（图中虚线所示）.这两列波的频率相同，振动方向均沿y轴.则图中x=1、2、3、4、5、6、7、8各点中振幅最大的是x=__________的点，振幅最小的是x=___________的点.

图12-6-11

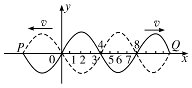
Answer 1

4和8  2和6

解析:

本题主要考查对波的叠加原理的理解及应用.由题可知，这两列波的频率相同，振动方向均沿y轴，故为相干波.设P、Q分别为两列波的波源，在图示时刻均沿y轴正向向上振动，则1、2、3、4、5、6、7、8到两相干波源P、Q的路程差分别为（设波长为λ）：

点1或点7：Δs₁=Δs₇=,

点2或点6：Δs₂=Δs₆=

点3或点5：Δs₃=Δs₅=

点4：Δs₄=λ-λ=0,

点8:Δs₈=.

根据两列相干波干涉时加强和减弱的条件知：点4和8位置的合振动振幅最大，点2和点6位置的合振动振幅最小.