题目内容
 电阻不计的足够长导轨竖直平行放置,导轨两端均接电阻R,导轨间的磁场的磁感应强度为B,导体棒AB质量为m,电阻为R,长度为L(等于导轨间距),与导轨接触良好,运动过程中,棒始终未达到导轨上端.
电阻不计的足够长导轨竖直平行放置,导轨两端均接电阻R,导轨间的磁场的磁感应强度为B,导体棒AB质量为m,电阻为R,长度为L(等于导轨间距),与导轨接触良好,运动过程中,棒始终未达到导轨上端.(1)若AB在竖直向上的恒力F作用下由静止开始运动,AB棒能达到的最大速度v=?
(2)若要使AB由静止以加速度a向上作匀加速直线运动,则F与t的关系是什么?写出F与t的关系式.
(3)若在(1)条件下棒从静止开始达到最大速度过程中,棒上升的高度为H,则此过程中导轨上端电阻R上产生的热量Q为多少?通过的电量q为多少?
分析:(1)当棒子加速度为零时,速度最大,根据共点力平衡,结合导体切割产生的感应电动势和闭合电路欧姆定律求出最大速度.
(2)根据牛顿第二定律结合安培力大小公式和闭合电路欧姆定律求出F与t的表达式.
(3)根据能量守恒定律求出整个回路产生的热量,抓住金属棒和电阻R产生的热量相等求出导轨上端电阻R产生的热量.根据q=
求出通过的电量.
(2)根据牛顿第二定律结合安培力大小公式和闭合电路欧姆定律求出F与t的表达式.
(3)根据能量守恒定律求出整个回路产生的热量,抓住金属棒和电阻R产生的热量相等求出导轨上端电阻R产生的热量.根据q=
| △Φ |
| 2R |
解答:解:(1)对棒由牛顿第二定律得:
F-mg-BIl=ma ①
又I=
②,所以棒向上做加速度减小的加速运动.
当a=0,即F=mg+
时③,速度最大
所以Vm=
④
(2)由F-mg-
=ma ⑤
及v=at ⑥得:
F与T的关系式为:F=m(g+a)+
t⑦
(3)设棒上升H过程:AB棒产生热量为Q′,在棒上升过程由能量守恒得:
FH=mgH+
mV2+Q+Q′⑧
又Q=Q′⑨
由⑧⑨两式得Q=
(F-mg)H-
⑩
通过的电量q=
=
.
答:(1)AB棒能达到的最大速度为
.
(2)使AB由静止以加速度a向上作匀加速直线运动,则F与t的关系为F=m(g+a)+
t.
(3)此过程中导轨上端电阻R上产生的热量Q=
(F-mg)H-
.通过的电量为
.
F-mg-BIl=ma ①
又I=
| BlV |
| 2R |
当a=0,即F=mg+
| B2l2v |
| 2R |
所以Vm=
| 2(F-mg)R |
| B2l2 |
(2)由F-mg-
| B2l2v |
| 2R |
及v=at ⑥得:
F与T的关系式为:F=m(g+a)+
| B2l2a |
| 2R |
(3)设棒上升H过程:AB棒产生热量为Q′,在棒上升过程由能量守恒得:
FH=mgH+
| 1 |
| 2 |
又Q=Q′⑨
由⑧⑨两式得Q=
| 1 |
| 2 |
| m(F-mg)2R2 |
| B4l4 |
通过的电量q=
| △Φ |
| 2R |
| BLH |
| 2R |
答:(1)AB棒能达到的最大速度为
| 2(F-mg)R |
| B2l2 |
(2)使AB由静止以加速度a向上作匀加速直线运动,则F与t的关系为F=m(g+a)+
| B2l2a |
| 2R |
(3)此过程中导轨上端电阻R上产生的热量Q=
| 1 |
| 2 |
| m(F-mg)2R2 |
| B4l4 |
| BLH |
| 2R |
点评:本题考查了牛顿运动定律、闭合电路殴姆定律,安培力公式、感应电动势公式.同时当金属棒速度达到稳定时,则一定是处于平衡状态,

练习册系列答案
相关题目
 (2009?上海模拟)如图所示,两电阻不计的足够长光滑平行金属导轨与水平面夹角θ,导轨间距l,所在平面的正方形区域abcd内存在有界匀强磁场,磁感应强度为B,方向垂直斜面向上.将甲乙两电阻阻值相同、质量均为m的相同金属杆如图放置在导轨上,甲金属杆处在磁场的上边界,甲乙相距 l.静止释放两金属杆的同时,在甲金属杆上施加一个沿着导轨的外力F,使甲金属杆在运动过程中始终做沿导轨向下的匀加速直线运动,加速度大小gsinθ.
(2009?上海模拟)如图所示,两电阻不计的足够长光滑平行金属导轨与水平面夹角θ,导轨间距l,所在平面的正方形区域abcd内存在有界匀强磁场,磁感应强度为B,方向垂直斜面向上.将甲乙两电阻阻值相同、质量均为m的相同金属杆如图放置在导轨上,甲金属杆处在磁场的上边界,甲乙相距 l.静止释放两金属杆的同时,在甲金属杆上施加一个沿着导轨的外力F,使甲金属杆在运动过程中始终做沿导轨向下的匀加速直线运动,加速度大小gsinθ.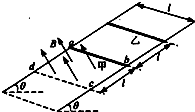 如图所示,电阻不计的足够长光滑平行金属导轨与水平面夹角为θ,导轨间距为l,轨道所在平面的正方形区域如耐内存在着有界匀强磁场,磁感应强度大小为B,方向垂直于导轨平面向上.电阻相同、质量均为m的两根相同金属杆甲和乙放置在导轨上,甲金属杆恰好处在磁场的上边界处,甲、乙相距也为l.在静止释放两金属杆的同时,对甲施加一沿导轨平面且垂直甲金属杆的外力,使甲在沿导轨向下的运动过程中始终以加速度a=gsinθ做匀加速直线运动,金属杆乙剐进入磁场时即做匀速运动.
如图所示,电阻不计的足够长光滑平行金属导轨与水平面夹角为θ,导轨间距为l,轨道所在平面的正方形区域如耐内存在着有界匀强磁场,磁感应强度大小为B,方向垂直于导轨平面向上.电阻相同、质量均为m的两根相同金属杆甲和乙放置在导轨上,甲金属杆恰好处在磁场的上边界处,甲、乙相距也为l.在静止释放两金属杆的同时,对甲施加一沿导轨平面且垂直甲金属杆的外力,使甲在沿导轨向下的运动过程中始终以加速度a=gsinθ做匀加速直线运动,金属杆乙剐进入磁场时即做匀速运动.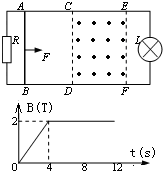 如图所示,水平面上有两电阻不计的足够长的光滑金属导轨平行固定放置,间距d为0.5m,左端通过导线与阻值为2Ω的电阻R连接,右端通过导线与阻值为4Ω的小灯泡L连接,在CDEF矩形区域内有竖直向上的匀强磁场,CE长为2m,CDEF区域内磁场的磁感应强度B随时间变化如图所示,在t=0时,一阻值为2Ω的金属棒在恒力F作用下由静止开始从AB位置沿导轨向右运动,当金属棒从AB位置运动到EF位置过程中,小灯泡的亮度没有发生变化,求:
如图所示,水平面上有两电阻不计的足够长的光滑金属导轨平行固定放置,间距d为0.5m,左端通过导线与阻值为2Ω的电阻R连接,右端通过导线与阻值为4Ω的小灯泡L连接,在CDEF矩形区域内有竖直向上的匀强磁场,CE长为2m,CDEF区域内磁场的磁感应强度B随时间变化如图所示,在t=0时,一阻值为2Ω的金属棒在恒力F作用下由静止开始从AB位置沿导轨向右运动,当金属棒从AB位置运动到EF位置过程中,小灯泡的亮度没有发生变化,求: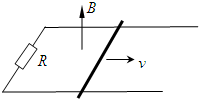 (2013?马鞍山三模)如图所示,间距为L、电阻不计的足够长平行光滑金属导轨水平放置,导轨左端用一阻值为R的电阻连接,导轨上横跨一根质量为m、电阻也为R的金属棒,金属棒与导轨接触良好.整个装置处于竖直向上、磁感应强度为B的匀强磁场中.现使金属棒以初速度v沿导轨向右运动,若金属棒在整个运动过程中通过的电荷量为q.下列说法正确的是( )
(2013?马鞍山三模)如图所示,间距为L、电阻不计的足够长平行光滑金属导轨水平放置,导轨左端用一阻值为R的电阻连接,导轨上横跨一根质量为m、电阻也为R的金属棒,金属棒与导轨接触良好.整个装置处于竖直向上、磁感应强度为B的匀强磁场中.现使金属棒以初速度v沿导轨向右运动,若金属棒在整个运动过程中通过的电荷量为q.下列说法正确的是( )