题目内容
3.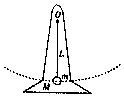 如图所示,支架连同电动机的质量为M(电动机在图中未画出),电动机装在支架上,支架放在水平地面上,转轴O处用长为L的轻杆悬挂一质量为m的小球,转轴在电动机带动下使轻杆及小球在竖直面内做匀速圆周运动,小球运动到最高点时,支架对地面恰好无压力,求:
如图所示,支架连同电动机的质量为M(电动机在图中未画出),电动机装在支架上,支架放在水平地面上,转轴O处用长为L的轻杆悬挂一质量为m的小球,转轴在电动机带动下使轻杆及小球在竖直面内做匀速圆周运动,小球运动到最高点时,支架对地面恰好无压力,求:(1)小球运动的向心加速度大小;
(2)小球运动的线速度大小;
(3)小球运动到最低点时地面对支架的支持力大小.
分析 (1)支架对地面无压力,所以绳子的拉力等于支架的重力,由牛顿第二定律即可求出向心加速度.
(2)支架对地面无压力,所以绳子的拉力等于支架的重力,由向心力公式求出此时小球速度.
(3)先求出小球在最低点时对绳子的拉力,然后对支架进行受力分析即可求出.
解答 解:(1)小球运动到最高点时,支架对地面恰好无压力,则绳子的拉力T=Mg,
小球运动过程中最高点时绳子的拉力与重力一起提供向心力,由牛顿第二定律得:Mg+mg=ma
所以:a=$\frac{Mg+mg}{m}$
(2)小球运动过程中最高点时绳子的拉力与重力一起提供向心力,则:Mg+mg=m$\frac{{v}^{2}}{L}$
所以:v=$\sqrt{\frac{MgL+mgL}{m}}$
(3)球在最低点时,应用牛顿第二定律,得:
T1-mg=ma
绳子的拉力:T1=mg+ma=Mg+2mg
支架受到的支持力:N=Mg+T1=(2M+2m)g
由牛顿第三定律可知支架对地面的压力为(2M+2m)g
答:(1)小球运动的向心加速度大小是$\frac{Mg+mg}{m}$;
(2)小球运动的线速度大小$\sqrt{\frac{MgL+mgL}{m}}$;
(3)小球运动到最低点时地面对支架的支持力大小(2M+2m)g.
点评 本题主要考查了动能定理和圆周运动公式的灵活运用,注意过程的选取,然后利用牛顿第三定律求的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.伽利略根据小球在斜面上运动的实验和理想实验,提出了惯性的概念,从而奠定了牛顿力学的基础.早期物理学家关于惯性有下列说法,其中正确的是( )
| A. | 没有力作用,物体只能处于静止状态 | |
| B. | 物体抵抗运动状态变化的性质是惯性 | |
| C. | 行星在圆周轨道上保持匀速率运动的性质是惯性 | |
| D. | 运动物体如果没有受到力的作用,物体可能做匀速圆周运动 |
11.关于质点,下列说法正确的是( )
| A. | 质量和体积都很小的物体才能看作质点 | |
| B. | 在直线运动中,位移的大小和路程一定相同 | |
| C. | 刘翔夺得了110m栏冠军是因为平均速度大 | |
| D. | 中央电视台每晚新闻联播节目19:00开播指的是时间间隔 |
4.我们研究的带电粒子是指那些受到的电场力远大于重力的粒子.下列粒子不能忽略重力的是( )
| A. | 电子 | B. | 质子 | C. | 氧离子 | D. | 带电小球 |
11.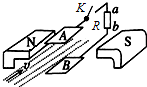 如图表示磁流体的发电原理:将一束等离子体(重力不计)沿图示方向以速度v喷射入磁场,金属板A、B就形成一个直流电源,设磁感应强度为B,金属板A、B相距d,外接电阻R,A、B间弥漫的电离气体电阻为r.则下述说法正确的是( )
如图表示磁流体的发电原理:将一束等离子体(重力不计)沿图示方向以速度v喷射入磁场,金属板A、B就形成一个直流电源,设磁感应强度为B,金属板A、B相距d,外接电阻R,A、B间弥漫的电离气体电阻为r.则下述说法正确的是( )
 如图表示磁流体的发电原理:将一束等离子体(重力不计)沿图示方向以速度v喷射入磁场,金属板A、B就形成一个直流电源,设磁感应强度为B,金属板A、B相距d,外接电阻R,A、B间弥漫的电离气体电阻为r.则下述说法正确的是( )
如图表示磁流体的发电原理:将一束等离子体(重力不计)沿图示方向以速度v喷射入磁场,金属板A、B就形成一个直流电源,设磁感应强度为B,金属板A、B相距d,外接电阻R,A、B间弥漫的电离气体电阻为r.则下述说法正确的是( )| A. | 金属板A为电源的正极 | |
| B. | 开关断开时,金属板间的电势差为Bvd | |
| C. | 开关闭合后,金属板间的电势差为$\frac{BvdR}{R+r}$ | |
| D. | 等离子体发生偏转的原因是洛伦兹力大于所受电场力 |
8. 如图所示,A、B为两块平行金属板,板长为l,两板间的距离为d,且d<<l,B板接地,A板的电势U可随时间发生突变,质量为m、电量为q的带正电粒子,从A的边缘贴近A板以平行于A板的初速度v0射入两板间的空间中,这时U=U0>0;经过一段时间t1,U突变为U=-U0;再经过一段时间t2,U又突变为U=U0;再经过一段时间t3,粒子又贴近A板且沿平行于A板的方向从A板的另一边缘处以速度v0射出两板间的空间,已知粒子在运动过程中曾非常接近B板但恰好没有B板接触,不计重力,则( )
如图所示,A、B为两块平行金属板,板长为l,两板间的距离为d,且d<<l,B板接地,A板的电势U可随时间发生突变,质量为m、电量为q的带正电粒子,从A的边缘贴近A板以平行于A板的初速度v0射入两板间的空间中,这时U=U0>0;经过一段时间t1,U突变为U=-U0;再经过一段时间t2,U又突变为U=U0;再经过一段时间t3,粒子又贴近A板且沿平行于A板的方向从A板的另一边缘处以速度v0射出两板间的空间,已知粒子在运动过程中曾非常接近B板但恰好没有B板接触,不计重力,则( )
 如图所示,A、B为两块平行金属板,板长为l,两板间的距离为d,且d<<l,B板接地,A板的电势U可随时间发生突变,质量为m、电量为q的带正电粒子,从A的边缘贴近A板以平行于A板的初速度v0射入两板间的空间中,这时U=U0>0;经过一段时间t1,U突变为U=-U0;再经过一段时间t2,U又突变为U=U0;再经过一段时间t3,粒子又贴近A板且沿平行于A板的方向从A板的另一边缘处以速度v0射出两板间的空间,已知粒子在运动过程中曾非常接近B板但恰好没有B板接触,不计重力,则( )
如图所示,A、B为两块平行金属板,板长为l,两板间的距离为d,且d<<l,B板接地,A板的电势U可随时间发生突变,质量为m、电量为q的带正电粒子,从A的边缘贴近A板以平行于A板的初速度v0射入两板间的空间中,这时U=U0>0;经过一段时间t1,U突变为U=-U0;再经过一段时间t2,U又突变为U=U0;再经过一段时间t3,粒子又贴近A板且沿平行于A板的方向从A板的另一边缘处以速度v0射出两板间的空间,已知粒子在运动过程中曾非常接近B板但恰好没有B板接触,不计重力,则( )| A. | t1=$\frac{l}{4{v}_{0}}$ | B. | t2=$\frac{l}{2{v}_{0}}$ | ||
| C. | U0=$\frac{8{mv}_{0}^{2}{d}^{2}}{q{l}^{2}}$ | D. | U0=$\frac{16{mv}_{0}^{2}{d}^{2}}{q{l}^{2}}$ |
9.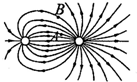 两点电荷激发的电场所形成的电场线分布如图所示,A、B是电场线上的两点,下列判断正确的是( )
两点电荷激发的电场所形成的电场线分布如图所示,A、B是电场线上的两点,下列判断正确的是( )
 两点电荷激发的电场所形成的电场线分布如图所示,A、B是电场线上的两点,下列判断正确的是( )
两点电荷激发的电场所形成的电场线分布如图所示,A、B是电场线上的两点,下列判断正确的是( )| A. | A点的电势高于B点的电势 | |
| B. | 左边点电荷带负电,右边点电荷带正电 | |
| C. | 两点电荷所带电荷量相等 | |
| D. | A点的电场强度大于B点的电场强度 |