题目内容
13.某星球的半径为R,在该星球表面某一倾角为θ的山坡上以初速度v0平抛一物体,经过时间t该物体落到山坡上.(1)求该星球的环绕速度;
(2)若在距离该星球表面高h处有一颗卫星绕着星球做匀速圆周运动,问:卫星运行的周期是多少?(不计一切阻力)
分析 (1)根据平抛运动规律列出水平方向和竖直方向的位移等式,结合几何关系求出重力加速度.忽略地球自转的影响,根据万有引力等于重力列出等式.
使物体绕着星球表面做匀速圆周运动,由万有引力定律充当向心力可求得环绕速度.
(2)由万有引力提供向心力即可求出在距离该星球表面高h处的周期.
解答 解:(1)由题意可知,是要求该星球上的“近地卫星”的绕行速度,也即为第一宇宙速度.设该星球表面处的重力加速度为g,由平抛运动规律可得:
tanθ=$\frac{y}{x}$,y=$\frac{1}{2}$gt2,x=v0t,
联立解得:g=$\frac{{2v_0^{\;}}}{t}$tanθ
对于绕该星球做匀速圆周运动的“近地卫星”,应有:mg=m $\frac{v^2}{R}$
解得:v=$\sqrt{gR}$=$\sqrt{\frac{{2{v_0}Rtanθ}}{t}}$
(2)由万有引力提供向心力:$\frac{GMm}{{{{(R+h)}^2}}}=m\frac{{4{π^2}(R+h)}}{T^2}$
推得:$T=\sqrt{\frac{{4{π^2}{{(R+h)}^3}}}{GM}}$
又 $\frac{GMm}{R^2}=mg$
有GM=gR2
所以有:$T=\sqrt{\frac{{4{π^2}{{(R+h)}^3}}}{{g{R^2}}}}=\frac{2π(R+h)}{R}\sqrt{\frac{t(R+h)}{{2{v_0}tanθ}}}$
答:(1)该星球的环绕速度是$\sqrt{\frac{{2{v_0}Rtanθ}}{t}}$;
(2)若在距离该星球表面高h处有一颗卫星绕着星球做匀速圆周运动,卫星运行的周期是$\frac{2π(R+h)}{R}\sqrt{\frac{t(R+h)}{2{v}_{0}tanθ}}$.
点评 处理平抛运动的思路就是分解.重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量.

| A. | 卡文迪许发现了万有引力定律 | |
| B. | 奥斯特首先提出用电场线来描绘电场 | |
| C. | 密立根通过对摩擦起电的研究测定了元电荷的电荷量 | |
| D. | 麦克斯韦建立了电磁场理论,并提出光也是一种电磁波 |
 在真空中同一直线上的A、B处分别固定电量分别为+2Q、-Q的两电荷.如图所示,若在A、B所在直线上放入第三个电荷C,只在电场力作用下三个电荷都处于平衡状态,则C的电性及位置是( )
在真空中同一直线上的A、B处分别固定电量分别为+2Q、-Q的两电荷.如图所示,若在A、B所在直线上放入第三个电荷C,只在电场力作用下三个电荷都处于平衡状态,则C的电性及位置是( )| A. | 正电,在A、B之间 | B. | 正电,在B点右侧 | C. | 负电,在B点右侧 | D. | 负电,在A点左侧 |
| A. | 5m、1.8m | B. | 6.8m、3.2m | C. | 5m、3.2m | D. | 6.8m、5m |
| A. | 平均速率大 | B. | 平均速度大 | ||
| C. | 冲刺时的瞬时速度大 | D. | 某一时刻的瞬时速度大 |
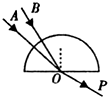 如图所示,两束频率不同的光束A和B分别沿半径方向射入半圆形玻璃砖,出射光线都是OP方向.下面关于A光和B光的比较中,说法不正确的是( )
如图所示,两束频率不同的光束A和B分别沿半径方向射入半圆形玻璃砖,出射光线都是OP方向.下面关于A光和B光的比较中,说法不正确的是( )| A. | 玻璃对A 光的折射率更大 | |
| B. | 真空中A光的波长更长 | |
| C. | A光由玻璃射向空气的全反射临界角更大 | |
| D. | 玻璃中A光的传播速度更大 |
| A. | 抢险队员到达对岸的最短时间是20s,这一时间与河水速度大小是否变化无关 | |
| B. | 随着河水速度大小的变化,船到达对岸的最短时间会相应变化 | |
| C. | 若冲锋舟的船头始终垂直于河岸,当它距离岸40m处的河水速度大小是3m/s,则此时船的实际速度是5m/s | |
| D. | 无论河水速度多大,也无论抢险队员怎样调整船的航向,冲锋舟都无法到达河对岸 |
| A. | 两个物体相互接触一定会产生弹力 | |
| B. | 用一根线竖直悬挂的物体静止时,线拉力方向所在的直线一定通过物体的重心 | |
| C. | 舞蹈演员在做各种优美的动作时,其重心在体内位置不变 | |
| D. | 弹力的大小与物体的形变程度有关,形变程度越大,弹力越大 |
| A. | 第 1s 内的位移是 8m | B. | 前 2s 内的平均速度是 6m/s | ||
| C. | 任意相邻 1s 内的位移差都是 1m | D. | 任意 1s 内的速度增量都是2m/s |