题目内容
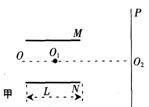
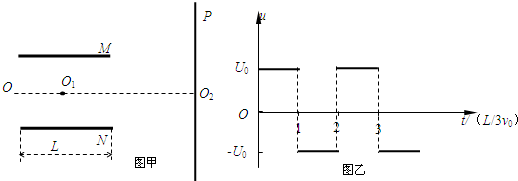
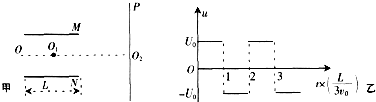
如图甲所示,M和N是相互平行的金属板,OO1O2为中线,O1为板间区域的中点,P是足够大的荧光屏.带电粒子连续地从O点沿OO1方向射入两板间.
(1)若两板间只存在一个以O1点为圆心的圆形匀强磁场区域,磁场方向垂直纸面向里,已知磁感应强度B=0.50T,两板间距
d=
cm,板长L=1.0cm,带电粒子质量m=2.0×10-25kg,电量q=8.0×10-18C,入射速度v=
×105m/s.若能在荧光屏上观察到亮点,试求粒子在磁场中运动的轨道半径r,并确定磁场区域的半径R应满足的条件.
(2)若只在两板间加恒定电压U,M和N相距为d,板长为L(不考虑电场边缘效应).若入射粒子是电量为e、质量为m的电子,它们的速度v满足0<v≤v0,试求打在荧光屏P上偏离点O2最远的粒子的动能.
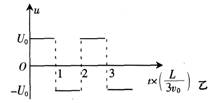
(3)若只在两板间加如图乙所示的交变电压u,M和N相距为d,板长为L(不考虑电场边缘效应).入射粒子是电量为e、质量为m的电子.某电子在t0=L/4v0时刻以速度v0射入电场,要使该电子能通过平行金属板,试确定U0应满足的条件.
(1)若两板间只存在一个以O1点为圆心的圆形匀强磁场区域,磁场方向垂直纸面向里,已知磁感应强度B=0.50T,两板间距
d=
| 3 |
| 3 |
(2)若只在两板间加恒定电压U,M和N相距为d,板长为L(不考虑电场边缘效应).若入射粒子是电量为e、质量为m的电子,它们的速度v满足0<v≤v0,试求打在荧光屏P上偏离点O2最远的粒子的动能.
(3)若只在两板间加如图乙所示的交变电压u,M和N相距为d,板长为L(不考虑电场边缘效应).入射粒子是电量为e、质量为m的电子.某电子在t0=L/4v0时刻以速度v0射入电场,要使该电子能通过平行金属板,试确定U0应满足的条件.

分析:(1)带电粒子射入磁场中做匀速圆周运动,由洛伦兹力充当向心力,由牛顿第二定律求出粒子的轨迹半径r.若恰好在荧光屏P上观察到亮点时,粒子偏转角最大,磁场区域的半径最大,由几何知识求出磁场区域半径R的最大值,即可得到条件.
(2)若只在两板间加恒定电压U,带电粒子射入电场中做类平抛运动,运用运动的分解,根据牛顿第二定律、运动学公式和动能定理结合求在荧光屏P上偏离点O2最远的粒子的动能.
(3)当加上交变电压时,分析粒子的运动情况,由牛顿第二定律求出加速度,由水平方向匀速运动,求出粒子通过电场的时间,由运动学公式分分段求在这个时间内,粒子在垂直于极板方向偏转的距离之和,当该偏转距离之和小于等于
时,粒子能飞出电场.
(2)若只在两板间加恒定电压U,带电粒子射入电场中做类平抛运动,运用运动的分解,根据牛顿第二定律、运动学公式和动能定理结合求在荧光屏P上偏离点O2最远的粒子的动能.
(3)当加上交变电压时,分析粒子的运动情况,由牛顿第二定律求出加速度,由水平方向匀速运动,求出粒子通过电场的时间,由运动学公式分分段求在这个时间内,粒子在垂直于极板方向偏转的距离之和,当该偏转距离之和小于等于
| d |
| 2 |
解答:解:(1)由牛顿第二定律可知:qvB=m
代入数据解得
粒子在磁场中运动的轨道半径r=5
×10-3m=8.7×10-3m
如图所示,设恰好在荧光屏P上观察到亮点时,粒子偏转角为2θ,磁场区域的最大半径为R0,由几何关系可知
tan2θ=
=
而tanθ=
代入数据解得 R0=5×10-3m
则R应满足的条件 R≤5×10-3m
(2)电子在两极板间的加速度a=
通过金属板的时间 t=
对打在荧光屏P上偏离点O2最远的粒子有
=
at2
此时粒子的动能 Ek=
eU+
mv2
联列解得 Ek=
(3)交变电压的周期,则 T=
,则t0=
T
电子通过金属板的时间 t′=
=
T
电子在两极板间的加速度 a′=
设电子分别在
T~
T、
T~
T、
T~
T、
T~
T~~时间内沿垂直于初速度方向运动的位移依次为y1、y2、y3、y4,则有
y1=y3=-a′(
-t0)2
y2=a′(
T)2
y4=
a′(
)2
要使电子能通过平行金属板,应满足条件:y1+y2+y3+y4≤
联立解得U0≤
答:
(1)粒子在磁场中运动的轨道半径r是8.7×10-3m,磁场区域的半径R应满足的条件是R≤5×10-3m.
(2)打在荧光屏P上偏离点O2最远的粒子的动能是
.
(3)要使该电子能通过平行金属板,U0≤
.
| v2 |
| r |

代入数据解得
粒子在磁场中运动的轨道半径r=5
| 3 |
如图所示,设恰好在荧光屏P上观察到亮点时,粒子偏转角为2θ,磁场区域的最大半径为R0,由几何关系可知
tan2θ=
| ||
|
| d |
| L |
而tanθ=
| R0 |
| r |
代入数据解得 R0=5×10-3m
则R应满足的条件 R≤5×10-3m
(2)电子在两极板间的加速度a=
| eU |
| md |
通过金属板的时间 t=
| L |
| v |
对打在荧光屏P上偏离点O2最远的粒子有
| d |
| 2 |
| 1 |
| 2 |
此时粒子的动能 Ek=
| 1 |
| 2 |
| 1 |
| 2 |
联列解得 Ek=
| eU(d2+L2) |
| 2d2 |
(3)交变电压的周期,则 T=
| 2L |
| 3v0 |
| 3 |
| 8 |
电子通过金属板的时间 t′=
| L |
| v0 |
| 3 |
| 2 |
电子在两极板间的加速度 a′=
| eU0 |
| md |
设电子分别在
| 3 |
| 8 |
| 5 |
| 8 |
| 5 |
| 8 |
| 11 |
| 8 |
| 11 |
| 8 |
| 13 |
| 8 |
| 13 |
| 8 |
| 15 |
| 8 |
y1=y3=-a′(
| T |
| 2 |
y2=a′(
| 3 |
| 8 |
y4=
| 1 |
| 2 |
| T |
| 4 |
要使电子能通过平行金属板,应满足条件:y1+y2+y3+y4≤
| d |
| 2 |
联立解得U0≤
8md2
| ||
| eL2 |
答:
(1)粒子在磁场中运动的轨道半径r是8.7×10-3m,磁场区域的半径R应满足的条件是R≤5×10-3m.
(2)打在荧光屏P上偏离点O2最远的粒子的动能是
| eU(d2+L2) |
| 2d2 |
(3)要使该电子能通过平行金属板,U0≤
8md2
| ||
| eL2 |
点评:本题中带电粒子在磁场中圆周运动时,画出轨迹,运用几何知识求磁场区域的半径,电场中类平抛运动,运用运动的分解法进行处理,都是常用的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 cm,板长L=1.0cm,带电粒子质量m=2.0×10-25kg,电量q=8.0×10-18C,入射速度v =
cm,板长L=1.0cm,带电粒子质量m=2.0×10-25kg,电量q=8.0×10-18C,入射速度v =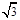 ×105m/s.若能在荧光屏上观察到亮点,试求粒子在磁场中运动的轨道半径r,并确定磁场区域的半径R应满足的条件.
×105m/s.若能在荧光屏上观察到亮点,试求粒子在磁场中运动的轨道半径r,并确定磁场区域的半径R应满足的条件.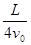 时刻以速度v0射入电场,要使该电子能通过平行金属板,试确定U0应满足的条件.
时刻以速度v0射入电场,要使该电子能通过平行金属板,试确定U0应满足的条件.