题目内容
如图所示,质量为m的物块沿着倾角为θ的斜面向下运动。对物块施加一个竖直向下的恒力F后( ) 
| A.原来匀速运动的,仍做匀速运动 |
| B.原来匀速运动的,将改做加速运动 |
| C.原来匀加速运动的,加F后加速度不变 |
| D.原来匀加速运动的,加F后加速度变大 |
AD
解析试题分析:如果原来是匀速运动,则加F前有:mgsinθ-µmgcosθ=0,得sinθ-µcosθ=0;加F后有:(mgsinθ+Fsinθ)-µ(mgcosθ+Fcosθ)=ma,计算后得F(sinθ-µcosθ)=ma,则a=0,说明加F后物体仍做匀速运动,所以A选项正确;如果原来是匀加速运动,则加F前有:mgsinθ-µmgcosθ=ma,得sinθ-µcosθ=a/g;加F后有:(mgsinθ+Fsinθ)-µ(mgcosθ+Fcosθ)=ma‘,整理后得(mgsinθ-µmgcosθ)+F(sinθ-µcosθ)=ma‘,计算后有:a’=a+Fa/mg,所以加F后加速度增加,D选项正确。
考点:本题考查物体的平衡条件和牛顿第二定律的应用。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案如图所示,某人通过定滑轮拉住一重物,当人向右跨出一步后,人与物仍保持静止,则 ( )
| A.地面对人的摩擦力减小 |
| B.地面对人的摩擦力不变 |
| C.人对地面的压力增大 |
| D.人对地面的压力减小 |
如图所示,物体a、b和c叠放在水平桌面上,水平力Fb=5 N,Fc=10 N分别作用于物体b、c上,a、b和c仍保持静止,以f1、f2、f3分别表示a与b、b与c、c与桌面间的静摩擦力的大小,则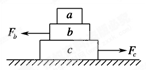
| A.f1=5 N,f2=0,f3=5 N | B.f1=5 N,f2=5 N,f3=0 |
| C.f1=0,f2=5 N,f3=5 N | D.f1=0,f2=10 N,f3=5 N |
用两个相同的足够大的水平力F将100个完全相同的木块夹在两个相同的竖直木板之间,所有木块都如图所示保持静止状态,每个木块的质量都为m,图中所有的接触面的动摩擦因素都为μ ,则编号57和58号木块之间的摩擦力的大小为:(木块从左至右编号依次为1、2、…、99、100) ( )
| A.mg | B.7mg | C.8mg | D.μF/100 |
作用于O点的三力平衡,设其中一个力的大小为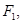 沿y轴正方向,力
沿y轴正方向,力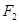 大小未知,与x轴负方向夹角为
大小未知,与x轴负方向夹角为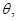 如图所示,下列关于第三个力
如图所示,下列关于第三个力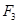 的判断正确的是
的判断正确的是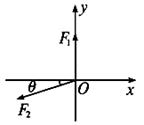
A.力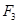 只能在第四象限 只能在第四象限 |
B.力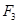 与 与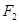 夹角变小,但 夹角变小,但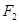 和 和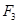 的合力不变 的合力不变 |
C.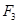 的最小值为F2cos 的最小值为F2cos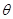 |
D.力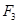 在第一象限的任意区域 在第一象限的任意区域 |
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态。现缓慢向上提上面的木块,直到它刚离开上面弹簧,在这过程中下面木块移动的距离为
| A.m1g/k1 | B.m2g/k1 | C.m1g/k2 | D.m2g/k2 |
如图所示,水平地面上有楔形物体b,b的斜面上有一小物块a,a与b之间、b与地面之间均存在摩擦。已知a恰好可沿斜面匀速下滑,此时若对a施加如图所示的作用力,a仍沿斜面下滑,则下列说法正确的是:AD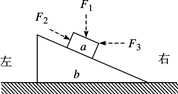
| A.在a上施加竖直向下的力F1,则地面对b无摩擦力 |
| B.在a上施加沿斜面向下的力F2,则地面对b的摩擦力水平向左 |
| C.在a上施加一个水平向左的力F3,则地面对b的摩擦力水平向右 |
| D.无论在a上施加什么方向的力,地面对b均无摩擦力 |
如图所示,轻杆BC的一端铰接于C,另一端悬挂重物G,并用细绳绕过定滑轮用力拉住。开始时, ,现用拉力F使
,现用拉力F使 缓慢减小,直到BC接近竖直位置的过程中,杆BC所受的压力
缓慢减小,直到BC接近竖直位置的过程中,杆BC所受的压力
| A.保持不变 | B.逐渐增大 | C.逐渐减小 | D.先增大后减小 |