题目内容
2.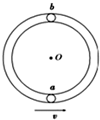 如图所示光滑管形圆轨道半径为R(管径远小 于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )
如图所示光滑管形圆轨道半径为R(管径远小 于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )| A. | 当小球b在最高点对轨道无压力时,小球a比小球b所需向心力大5mg | |
| B. | 当v=$\sqrt{5gR}$ 时,小球b在轨道最高点对轨道无压力 | |
| C. | 速度v至少为$\sqrt{5gR}$,才能使两球在管内做圆周运动 | |
| D. | 只要v≥$\sqrt{5gR}$,小球a对轨道最低点的压力比小球b对轨道最高点的压力大6mg |
分析 小球在圆环的内侧运动,相当于圆周运动中的杆的模型,此时在最高的速度是可以为零的,在整个运动的过程中小球的机械能守恒,可以求得小球到达最低端是的速度和需要的向心力的大小.
解答 解:AB、由于管中没有摩擦力的作用,所以球的机械能守恒,
当小球b在最高点对轨道无压力,即只有重力做为向心力,
所以mg=m$\frac{{v}_{b}^{2}}{R}$,所以在最高点时b球的速度的大小为$\sqrt{gR}$,
从最高点到最低点,由机械能守恒可得,mg•2R+$\frac{1}{2}$mvb2=$\frac{1}{2}$mva2,
对于a球,在最低点是,由向心力的公式可得 F-mg=m$\frac{{v}_{a}^{2}}{R}$,
所以F-mg=5mg,F=6mg,v=va=$\sqrt{5gR}$,故B正确;
所以此时的向心力的大小为5mg,所以小球a比小球b所需向心力大4mg,故A错误;
C、由于最高点速度可以为零,根据动能定理知-2mgR=0-$\frac{1}{2}m{v}^{2}$,知v=2$\sqrt{gR}$,故C错误;
D、最高点时F1=m$\frac{{v}_{1}^{2}}{R}$-mg,
在最低点时,F2=m$\frac{{v}_{2}^{2}}{R}$+mg,
由机械能守恒有$\frac{1}{2}$mv12+mg2R=$\frac{1}{2}$mv22,
所以F2-F1=6mg.故D正确.
故选:BD
点评 内管可以对小球提供支持力,可化为轻杆模型,在最高点时,小球速度可以为零,与绳的模型一定要区分开.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.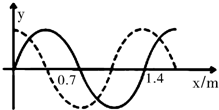 如图所示,图中的实线为一列简谐波在t时刻的图象,虚线为这列波在(t+0.21)s时刻的图象,则以下说法错误的是 ( )
如图所示,图中的实线为一列简谐波在t时刻的图象,虚线为这列波在(t+0.21)s时刻的图象,则以下说法错误的是 ( )
 如图所示,图中的实线为一列简谐波在t时刻的图象,虚线为这列波在(t+0.21)s时刻的图象,则以下说法错误的是 ( )
如图所示,图中的实线为一列简谐波在t时刻的图象,虚线为这列波在(t+0.21)s时刻的图象,则以下说法错误的是 ( )| A. | 波一定向右传播 | |
| B. | 若波向左传播,波速一定为5m/s | |
| C. | 若周期为0.84s,波一定向右传播 | |
| D. | 若周期小于0.84s,波也可能向左传播 | |
| E. | 波长等于1.4m |
13.关于万有引力公式F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,以下说法正确的是( )
| A. | 公式只适用于星球之间的引力计算,不适用于质量较小的物体 | |
| B. | 当两物体间的距离趋近于0时,万有引力趋近于无穷大 | |
| C. | 两物体间的万有引力也符合牛顿第三定律 | |
| D. | 公式适用于两质点;也适用于两个质量分布均匀的球体,r应取两球心间的距离 |
10.人造地球卫星绕地球做匀速圆周运动,轨道离地面越高该卫星( )
| A. | 所受的万有引力越小 | B. | 运行的角速度越大 | ||
| C. | 运行的线速度越大 | D. | 运行的周期越小 |
17. 神舟九号飞船于2012年6月16日从酒泉卫星发射中心发射升空,先后与天宫一号目标飞行器成功进行了自动和手动两次对接.图为对接前天宫一号、神舟九号飞船围绕地球沿圆轨道运行的示意图,下列说法中正确的是( )
神舟九号飞船于2012年6月16日从酒泉卫星发射中心发射升空,先后与天宫一号目标飞行器成功进行了自动和手动两次对接.图为对接前天宫一号、神舟九号飞船围绕地球沿圆轨道运行的示意图,下列说法中正确的是( )
 神舟九号飞船于2012年6月16日从酒泉卫星发射中心发射升空,先后与天宫一号目标飞行器成功进行了自动和手动两次对接.图为对接前天宫一号、神舟九号飞船围绕地球沿圆轨道运行的示意图,下列说法中正确的是( )
神舟九号飞船于2012年6月16日从酒泉卫星发射中心发射升空,先后与天宫一号目标飞行器成功进行了自动和手动两次对接.图为对接前天宫一号、神舟九号飞船围绕地球沿圆轨道运行的示意图,下列说法中正确的是( )| A. | 天宫一号的速率大于神舟九号飞船的速率 | |
| B. | 天宫一号的加速度大于神舟九号飞船的加速度 | |
| C. | 天宫一号的周期大于神舟九号飞船的周期 | |
| D. | 天宫一号的机械能一定小于神舟九号飞船的机械能 |
7.关于曲线运动,下列说法中正确的是( )
| A. | 做曲线运动的物体,速度大小时刻在改变,一定是变速运动 | |
| B. | 做曲线运动的物体,物体所受合外力方向与速度方向一定不在同一直线上,必有加速度 | |
| C. | 物体不受力或受到的合外力为零时,也可能做曲线运动 | |
| D. | 做曲线运动的物体可能处于平衡状态 |
14.牛顿以天体之间普遍存在着引力为依据,运用严密的逻辑推理,建立了万有引力定律.在牛顿创建万有引力定律的过程中,以下说法错误的是( )
| A. | 接受了胡克等科学家关于“吸引力与两中心距离的平方成反比”的猜想 | |
| B. | 根据地球上一切物体都以相同加速度下落的事实,得出物体受地球的引力与其质量成正比,即F∝m的结论 | |
| C. | 根据F∝m和牛顿第三定律,分析了地、月间的引力关系,进而得出F∝m1、m2 | |
| D. | 根据大量实验数据得出了比例系数G的大小 |
11.下列说法中正确的是( )
| A. | 居里夫人首先发现了天然放射现象 | |
| B. | 对天然放射现象的研究建立了原子的核式结构 | |
| C. | 压力和温度对放射性元素衰变的快慢没有任何影响 | |
| D. | 贝克勒耳通过对天然放射现象的研究,发现了质子和中子 |