题目内容
 (2007?广东)如图为装置的垂直截面图,虚线A1A2是垂直截面与磁场区边界面的交线,匀强磁场分布在A1A2的右侧区域,磁感应强度B=0.4T,方向垂直纸面向外,A1A2与垂直截面上的水平线夹角为45°.在A1A2左侧,固定的薄板和等大的挡板均水平放置,它们与垂直截面交线分别为S1、S2,相距L=0.2m.在薄板上P处开一小孔,P与A1A2线上点D的水平距离为L.在小孔处装一个电子快门.起初快门开启,一旦有带正电微粒通过小孔,快门立即关闭,此后每隔T=3.0×10-3s开启一次并瞬间关闭.从S1S2之间的某一位置水平发射一速度为v0的带正电微粒,它经过磁场区域后入射到P处小孔.通过小孔的微粒与档板发生碰撞而反弹,反弹速度大小是碰前的0.5倍.
(2007?广东)如图为装置的垂直截面图,虚线A1A2是垂直截面与磁场区边界面的交线,匀强磁场分布在A1A2的右侧区域,磁感应强度B=0.4T,方向垂直纸面向外,A1A2与垂直截面上的水平线夹角为45°.在A1A2左侧,固定的薄板和等大的挡板均水平放置,它们与垂直截面交线分别为S1、S2,相距L=0.2m.在薄板上P处开一小孔,P与A1A2线上点D的水平距离为L.在小孔处装一个电子快门.起初快门开启,一旦有带正电微粒通过小孔,快门立即关闭,此后每隔T=3.0×10-3s开启一次并瞬间关闭.从S1S2之间的某一位置水平发射一速度为v0的带正电微粒,它经过磁场区域后入射到P处小孔.通过小孔的微粒与档板发生碰撞而反弹,反弹速度大小是碰前的0.5倍.(1)通过一次反弹直接从小孔射出的微粒,其初速度v0应为多少?
(2)求上述微粒从最初水平射入磁场到第二次离开磁场的时间.(忽略微粒所受重力影响,碰撞过程无电荷转移.已知微粒的荷质比
| q | m |
分析:(1)根据洛伦兹力提供向心力求解半径,欲使微粒能进入小孔,半径r的取值范围为:L<r<2L,带入可求得速度范围,欲使进入小孔的微粒与挡板一次相碰返回后能通过小孔,还必须满足条件:
+
=nT其中n=1,2,3,…进而即可求得速度;
(2)画出粒子在磁场中运动的轨迹,根据周期公式求出在磁场中运动的周期,分别求出带电微粒第一次、第二次在磁场中运动的时间和第一次离开磁场运动到挡板的时间及碰撞后再返回磁场的时间为,总时间为4个时间时间之和.
| L |
| v0 |
| L |
| 0.5v0 |
(2)画出粒子在磁场中运动的轨迹,根据周期公式求出在磁场中运动的周期,分别求出带电微粒第一次、第二次在磁场中运动的时间和第一次离开磁场运动到挡板的时间及碰撞后再返回磁场的时间为,总时间为4个时间时间之和.
解答: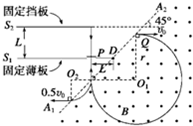 解:(1)如图所示,设带正电微粒在S1S2之间任意点Q以水平速度v0进入磁场,微粒受到的洛仑兹力为f,在磁场中做圆周运动的半径为r,有:
解:(1)如图所示,设带正电微粒在S1S2之间任意点Q以水平速度v0进入磁场,微粒受到的洛仑兹力为f,在磁场中做圆周运动的半径为r,有:
Bqv0=
解得:r=
欲使微粒能进入小孔,半径r的取值范围为:L<r<2L
代入数据得:80 m/s<v0<160 m/s
欲使进入小孔的微粒与挡板一次相碰返回后能通过小孔,还必须满足条件:
+
=nT其中n=1,2,3,…可知,只有n=2满足条件,即有:v0=100 m/s
(2)设微粒在磁场中做圆周运动的周期为T0,从水平进入磁场到第二次离开磁场的总时间为t,设t1、t4分别为带电微粒第一次、第二次在磁场中运动的时间,第一次离开磁场运动到挡板的时间为t2,碰撞后再返回磁场的时间为t3,运动轨迹如答图所示,则有:
T0=
; t1=
T0; t2=
; t3=
; t4=
T0
所以t=t1+t2+t3+t4=2.8×10-2s
答:(1)通过一次反弹直接从小孔射出的微粒,其初速度v0应为100 m/s;
(2)上述微粒从最初水平射入磁场到第二次离开磁场的时间为2.8×10-2s.
 解:(1)如图所示,设带正电微粒在S1S2之间任意点Q以水平速度v0进入磁场,微粒受到的洛仑兹力为f,在磁场中做圆周运动的半径为r,有:
解:(1)如图所示,设带正电微粒在S1S2之间任意点Q以水平速度v0进入磁场,微粒受到的洛仑兹力为f,在磁场中做圆周运动的半径为r,有:Bqv0=
| mv02 |
| r |
解得:r=
| mv0 |
| Bq |
欲使微粒能进入小孔,半径r的取值范围为:L<r<2L
代入数据得:80 m/s<v0<160 m/s
欲使进入小孔的微粒与挡板一次相碰返回后能通过小孔,还必须满足条件:
| L |
| v0 |
| L |
| 0.5v0 |
(2)设微粒在磁场中做圆周运动的周期为T0,从水平进入磁场到第二次离开磁场的总时间为t,设t1、t4分别为带电微粒第一次、第二次在磁场中运动的时间,第一次离开磁场运动到挡板的时间为t2,碰撞后再返回磁场的时间为t3,运动轨迹如答图所示,则有:
T0=
| 2πr |
| v0 |
| 3 |
| 4 |
| 2L |
| v0 |
| 4L |
| v0 |
| 1 |
| 4 |
所以t=t1+t2+t3+t4=2.8×10-2s
答:(1)通过一次反弹直接从小孔射出的微粒,其初速度v0应为100 m/s;
(2)上述微粒从最初水平射入磁场到第二次离开磁场的时间为2.8×10-2s.
点评:本题主要考查了带电粒子在磁场中做匀速圆周运动的问题,要求同学们能画出粒子运动的轨迹,正确分析带电微粒的运动过程,难度适中.

练习册系列答案
相关题目
 (2007?广东)如图所示的匀强电场E的区域内,由A、B、C、D、A′、B′、C′、D′作为顶点构成一正方体空间,电场方向与面ABCD垂直.下列说法正确的是( )
(2007?广东)如图所示的匀强电场E的区域内,由A、B、C、D、A′、B′、C′、D′作为顶点构成一正方体空间,电场方向与面ABCD垂直.下列说法正确的是( )
 (2007?广东)如图所示,在倾角为θ的固定光滑斜面上,质量为m的物体受外力F1和F2的作用,F1方向水平向右,F2方向竖直向上.若物体静止在斜面上,则下列关系正确的是( )
(2007?广东)如图所示,在倾角为θ的固定光滑斜面上,质量为m的物体受外力F1和F2的作用,F1方向水平向右,F2方向竖直向上.若物体静止在斜面上,则下列关系正确的是( ) (2007?广东)如图所示,在同一竖直面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L.小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生弹性碰撞,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O′与P的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求:
(2007?广东)如图所示,在同一竖直面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L.小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生弹性碰撞,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O′与P的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求: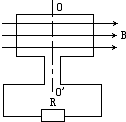 (2007?广东)如图所示,矩形线圈面积为S,匝数为N,内阻为r,绕OO′轴以角速度ω作匀速转动,在它从图示位置转过90°的过程中,下面说法正确的是( )
(2007?广东)如图所示,矩形线圈面积为S,匝数为N,内阻为r,绕OO′轴以角速度ω作匀速转动,在它从图示位置转过90°的过程中,下面说法正确的是( )