题目内容
13. 如图所示,有一条光滑轨道,其中一部分是水平的.一质量为2m的滑块A以vA=15m/s的速度向左滑行,另一质量为m的滑块B从5m高处由静止开始下滑,它们在水平轨道相碰后,B滑块刚好能返回到出发点.求碰撞后A的瞬时速度.(g取10m/s2)
如图所示,有一条光滑轨道,其中一部分是水平的.一质量为2m的滑块A以vA=15m/s的速度向左滑行,另一质量为m的滑块B从5m高处由静止开始下滑,它们在水平轨道相碰后,B滑块刚好能返回到出发点.求碰撞后A的瞬时速度.(g取10m/s2)
分析 B下滑的过程中只有重力做功,由机械能守恒定律求出B的速度;A与B碰撞的过程中水平方向系统不受力,应用动量守恒定律求出A的速度.
解答 解:物体从斜面上下滑时机械能守恒,由机械能守恒定律得:mgh=$\frac{1}{2}$mvB2,
解得:vB=$\sqrt{2gh}=\sqrt{2×10×5}=10$m/s,方向向右;
碰后B刚能回到B点,说明碰后B速度大小为vB′=10m/s,水平向左.
碰撞时A、B组成的系统动量守恒,设向左方向为正方向,由动量守恒定律可得:
mAvA-mBvB=mAvA′+mBvB′,
代入数据解得:vA′=5m/s,方向水平向左;
答:碰撞后A的瞬时速度大小是5m/s,方向向左.
点评 本题考查了求速度、判断碰撞类型,分析清楚物体运动过程、应用机械能守恒定律、动量守恒定律、知道碰撞类型即可正确解题.

练习册系列答案
相关题目
3.两个完全相同的金属小球,带电量之比为1:5,两带电小球可视为点电荷,在真空中相距为r时,相互作用力为F;若把它们接触后再放回原处,则它们之间的相互作用力可能为( )
| A. | $\frac{9}{5}F$ | B. | $\frac{5}{9}F$ | C. | $\frac{3}{5}F$ | D. | $\frac{4}{5}F$ |
4.质量和电荷量不同的带电粒子,在电场中由静止开始经相同电压加速后( )
| A. | 比荷大的粒子速度大,电荷量大的粒子动能大 | |
| B. | 比荷大的粒子动能大,电荷量大的粒子速度大 | |
| C. | 比荷大的粒子速度和动能都大 | |
| D. | 电荷量大的粒子速度和动能都大 |
1. 如图,有两个带有等量同种电荷的小球A和B,质量都是m,分别悬于长度为L的悬线一端,若使B球固定不动,并使OB在竖直方向上,A可以在竖直平面内自由摆动,由于静电斥力的作用,A球偏离B球的距离为x,为使A、B两球的距离缩短为$\frac{x}{2}$,可行的办法是( )
如图,有两个带有等量同种电荷的小球A和B,质量都是m,分别悬于长度为L的悬线一端,若使B球固定不动,并使OB在竖直方向上,A可以在竖直平面内自由摆动,由于静电斥力的作用,A球偏离B球的距离为x,为使A、B两球的距离缩短为$\frac{x}{2}$,可行的办法是( )
 如图,有两个带有等量同种电荷的小球A和B,质量都是m,分别悬于长度为L的悬线一端,若使B球固定不动,并使OB在竖直方向上,A可以在竖直平面内自由摆动,由于静电斥力的作用,A球偏离B球的距离为x,为使A、B两球的距离缩短为$\frac{x}{2}$,可行的办法是( )
如图,有两个带有等量同种电荷的小球A和B,质量都是m,分别悬于长度为L的悬线一端,若使B球固定不动,并使OB在竖直方向上,A可以在竖直平面内自由摆动,由于静电斥力的作用,A球偏离B球的距离为x,为使A、B两球的距离缩短为$\frac{x}{2}$,可行的办法是( )| A. | 使A的质量变为原来的2倍而A、B的带电量都减为原来的一半 | |
| B. | 只使A的带电量变为原来的一半,而其它条件不变 | |
| C. | 只使A球的质量变为原来的4倍,而其它条件不变 | |
| D. | 只使B球的带电量变为原来的$\frac{1}{8}$倍,而其它条件不变 |
8.关于点电荷的说法,正确的是( )
| A. | 只有体积很小的带电体,才能作为点电荷 | |
| B. | 点电荷一定是电量很小的电荷 | |
| C. | 当带电体本身的大小和电荷的分布对带电体之间的静电作用力没有影响或几乎没有影响时,就可以将他们看成点电荷 | |
| D. | 体积较大的电荷一定不能当作点电荷 |
5.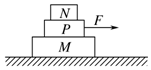 如图所示,在光滑的水平面上叠放着M、P、N三个物体,质量分别为m,2m和m,M、N、P间动摩擦因数均为μ,系统处于静止状态,现对P施加一个水平向右的拉力F,欲使P从M和N中拉出来,则F必须大于( )
如图所示,在光滑的水平面上叠放着M、P、N三个物体,质量分别为m,2m和m,M、N、P间动摩擦因数均为μ,系统处于静止状态,现对P施加一个水平向右的拉力F,欲使P从M和N中拉出来,则F必须大于( )
 如图所示,在光滑的水平面上叠放着M、P、N三个物体,质量分别为m,2m和m,M、N、P间动摩擦因数均为μ,系统处于静止状态,现对P施加一个水平向右的拉力F,欲使P从M和N中拉出来,则F必须大于( )
如图所示,在光滑的水平面上叠放着M、P、N三个物体,质量分别为m,2m和m,M、N、P间动摩擦因数均为μ,系统处于静止状态,现对P施加一个水平向右的拉力F,欲使P从M和N中拉出来,则F必须大于( )| A. | 4μmg | B. | 6μmg | C. | 10μmg | D. | 12μmg |
9.全国铁路大面积提速后,干线的部分区段时速可达300多公里,我们乘坐这样的列车就可以体验时速300多公里的追风感觉.火车转弯可以看成是在水平面内做匀速圆周运动,火车速度提高会使外轨受损.为解决火车高速转弯时外轨受损这一难题,以下措施可行的是( )
| A. | 适当减小外轨与内轨的高度差 | B. | 适当增加外轨与内轨的高度差 | ||
| C. | 适当减小弯道半径 | D. | 适当增大弯道半径 |
10.若地球一年自转一周(地球自转方向与公转方向一致),则下述说法可能正确的是( )
| A. | 赤道上人的体重将减小 | B. | 地球的同一面将永远面对太阳 | ||
| C. | 白天和黑夜将变得无限长 | D. | 地球上每处的白天长为半年 |
 如图所示,当磁铁突然向右靠近铜环运动时,铜环的运动情况是向右摆动(填“向左”、“向右”或“不”).
如图所示,当磁铁突然向右靠近铜环运动时,铜环的运动情况是向右摆动(填“向左”、“向右”或“不”).