题目内容
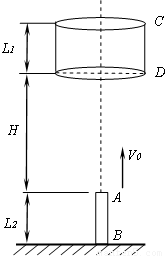
 悬空固定一个长l1=0.3m无底圆筒CD.现将一根长l2=0.24m的直杆AB在A端距圆筒CD底部H=5.46m处,从地面上以初速度v0=12m/s竖直上抛.如图所示,由于存在空气阻力,杆上升时加速度大小为a1=12m/s2,下降时加速度大小为a2=6.75m/s2.求:
悬空固定一个长l1=0.3m无底圆筒CD.现将一根长l2=0.24m的直杆AB在A端距圆筒CD底部H=5.46m处,从地面上以初速度v0=12m/s竖直上抛.如图所示,由于存在空气阻力,杆上升时加速度大小为a1=12m/s2,下降时加速度大小为a2=6.75m/s2.求:(1)AB杆上升H所用的时间tA;
(2)AB杆上升通过圆筒的时间t1为多少;
(3)AB杆从开始到t2=2s这一过程中的平均速度的大小.(保留2位有效数字)
分析:杆子上升过程跟竖直上抛类似,只不过加速度数值不同,规律完全相同;下降过程是初速度为零的匀加速直线运动.
解答:解:(1)上升过程中,A到达D点所经历的时间为tA,则有:H=v0tA-
a1
代入数据解得:tA=0.7s
(2)B到达C点所经历的时间为tB,则有:L1+L2+H=v0tB-
a1
联立方程解之得:tB=1s
所以AB杆上升通过圆筒的时间t1为:t1=tB-tA=0.3s
(3)杆AB向上穿过CD圆筒时瞬时速度,VB=V0-atB=0 刚好为零,由此判断杆AB刚好穿过圆筒.
杆下降1s通过的位移:h=
a2(t2-t1)2=
×6.75×12=3.375m
杆在2s内的总位移:x=L1+L2+H-h
杆在2s内的平均速度:
=
代入数据解得:
=
≈1.3m/s
答:(1)AB杆上升H所用的时间是0.7s;
(2)AB杆上升通过圆筒的时间t1为 0.3s;
(3)AB杆从开始到t2=2s这一过程中的平均速度的大小是1.3m/s.
| 1 |
| 2 |
| t | 2 A |
代入数据解得:tA=0.7s
(2)B到达C点所经历的时间为tB,则有:L1+L2+H=v0tB-
| 1 |
| 2 |
| t | 2 B |
联立方程解之得:tB=1s
所以AB杆上升通过圆筒的时间t1为:t1=tB-tA=0.3s
(3)杆AB向上穿过CD圆筒时瞬时速度,VB=V0-atB=0 刚好为零,由此判断杆AB刚好穿过圆筒.
杆下降1s通过的位移:h=
| 1 |
| 2 |
| 1 |
| 2 |
杆在2s内的总位移:x=L1+L2+H-h
杆在2s内的平均速度:
. |
| v |
| x |
| t2 |
代入数据解得:
. |
| v |
| 0.3+0.24+5.46-3.375 |
| 2 |
答:(1)AB杆上升H所用的时间是0.7s;
(2)AB杆上升通过圆筒的时间t1为 0.3s;
(3)AB杆从开始到t2=2s这一过程中的平均速度的大小是1.3m/s.
点评:杆子“自由落体”穿过圆筒的模型可分为:①杆子穿过圆筒②杆子穿过某一点③雨滴下落穿过窗台.都是基础的题型.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 悬空固定一个长l1=0.30m无底圆筒CD.现将一根长l2=0.24m的直杆AB在A端距圆筒CD底部H=5.46m处,从地面上以初速度v0=12m/s竖直上抛.如图所示,由于存在空气阻力,杆上升时加速度大小为a1=12.0m/s2,下降时加速度大小为a2=6.75m/s2.求
悬空固定一个长l1=0.30m无底圆筒CD.现将一根长l2=0.24m的直杆AB在A端距圆筒CD底部H=5.46m处,从地面上以初速度v0=12m/s竖直上抛.如图所示,由于存在空气阻力,杆上升时加速度大小为a1=12.0m/s2,下降时加速度大小为a2=6.75m/s2.求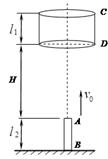
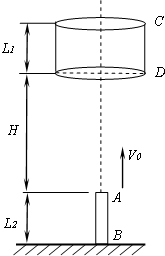 悬空固定一个长l1=0.30m无底圆筒CD.现将一根长l2=0.24m的直杆AB在A端距圆筒CD底部H=5.46m处,从地面上以初速度v0=12m/s竖直上抛.如图所示,由于存在空气阻力,杆上升时加速度大小为a1=12.0m/s2,下降时加速度大小为a2=6.75m/s2.求
悬空固定一个长l1=0.30m无底圆筒CD.现将一根长l2=0.24m的直杆AB在A端距圆筒CD底部H=5.46m处,从地面上以初速度v0=12m/s竖直上抛.如图所示,由于存在空气阻力,杆上升时加速度大小为a1=12.0m/s2,下降时加速度大小为a2=6.75m/s2.求