题目内容
7.一辆自行车从静止出发,开始以2m/s2的加速度做匀加速直线运动,经4s后运动方向不变改做匀速直线运动,匀速运动16s恰好到达终点,求:(1)加速过程中自行车运动的距离是多少?
(2)运动过程中最大的速度是多少?
(3)起点到终点的距离是多少?
分析 根据匀变速直线运动的位移时间公式求出加速过程中自行车运动的距离.根据速度时间公式求出运动过程中的最大速度.根据匀速运动的位移,结合匀加速运动的位移求出起点到终点的距离.
解答 解:(1)根据匀变速直线运动的位移时间公式得:${s_1}=\frac{1}{2}at_1^2$
代入数据解得:s1=$\frac{1}{2}×2×{4}^{2}$=16m
(2)根据速度时间公式得:v=at1
得:v=2×4m/s=8m/s
(3)匀速运动的位移为:
s2=vt2=8×16m=128m
起点到终点的距离为:
s=s1+s2=128+16m=144m.
答:(1)加速过程中自行车运动的距离是16m;
(2)运动过程中最大的速度是8m/s;
(3)起点到终点的距离是144m.
点评 解决本题的关键掌握匀变速直线运动的速度时间公式、位移时间公式,并能灵活运用,基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
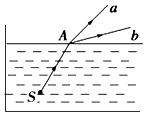
2.如图所示,水下光源S向水面A点发射一束光线,折射光线分别为a、b两束.则( )

| A. | a光的频率小于b光的频率 | |
| B. | 在真空中a光的速度大于b光的速度 | |
| C. | 若a光为绿光,则b可能为紫光 | |
| D. | 若保持入射点A位置不变,将入射光线瞬时针旋转,从水面上方观察,a光先消失 | |
| E. | 用同一双缝干涉实验装置分别用a、b光做实验,a光干涉相邻条纹间距大于b光干涉相邻条纹间距 |
16.物体静止在光滑水平面上.从某一时刻起用水平恒力F推物体,则在该力刚开始作用的瞬间( )
| A. | 立即产生加速度,但速度仍然为零 | B. | 立即产生速度,但加速度仍然为零 | ||
| C. | 立即同时产生加速度和速度 | D. | 速度和加速度均为零 |
17.在物理学的发展中,关于科学家和他们的贡献,下列说法中正确的是( )
| A. | 亚里士多德首先将实验事实和逻辑推理(包括数学推演)和谐地结合起来 | |
| B. | 哥白尼通过对行星观测记录的研究,发现了行星运动的三大定律 | |
| C. | 笛卡尔对牛顿第一定律的建立做出了贡献 | |
| D. | 库仑首次采用电场线的方法形象直观地描述电场,电流的磁效应是法拉第首次发现 |
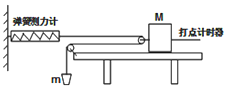 为了探究质量一定时加速度与力的关系,一同学设计了如图所示的实验装置,其中M为带滑轮的小车的质量,m为砂和砂桶的质量,(滑轮质量不计)
为了探究质量一定时加速度与力的关系,一同学设计了如图所示的实验装置,其中M为带滑轮的小车的质量,m为砂和砂桶的质量,(滑轮质量不计)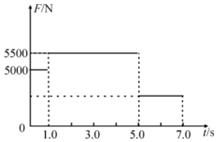 建筑工地上常用升降机将建材从地面提升到需要的高度,某次提升建材时,研究人员在升降机底板安装了压力传感器,可以显示建材对升降机底板压力的大小.已知建材放上升降机后,升降机先静止了t0=1s,然后启动,7s末刚好停止运动,在这7s内压力传感器的示数如图所示.当地重力加速度g取10m/s2.求:
建筑工地上常用升降机将建材从地面提升到需要的高度,某次提升建材时,研究人员在升降机底板安装了压力传感器,可以显示建材对升降机底板压力的大小.已知建材放上升降机后,升降机先静止了t0=1s,然后启动,7s末刚好停止运动,在这7s内压力传感器的示数如图所示.当地重力加速度g取10m/s2.求: