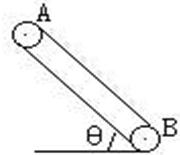
题目内容
如图所示，传递带与水平面夹角θ=37°，并以v0=10m/s的速度运行着，在传送带的A端轻轻地放一小物体。若已知该物体与传送带之间的滑动摩擦因数为μ=0.5，传送带A端到B端的距离S=16m，则小物体从A端运动到B端所需的时间可能是多少？（g=10m/s2）
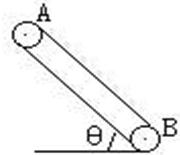
2s
解析:
当传送带以v=10m/s的速度向上运动时，上面分析还是正确的，小物体从A端运动到B端的时间为t1=4.0s。但是当传送带以v=10m/s的速度向下运动时，开始小物体的运动速度小于传送带的速度，它在传送带上下滑的加速度仍是
a2=gsinθ+μgcosθ=10m/s2，
经过t0=v/a2=1s时，小物体的运动速度大于传送带的速度，它所受摩擦力的方向发生突变，故t＞t0后，它又以加速度：a1=gsinθ-μgcosθ=2m/s2
加速下滑。在t0=1s内，小物体下滑的距离为：S0=（1／2）a2t02=5m
而在以后的时间内，下滑的距离为：S-S0=vt+（1/2）a1t2
解之得：t=1s或t=-11s
t=-11s不合题意，舍去。
小物体从A运动至B所需的时间为：t2=t0+t=2s，
练习册系列答案
相关题目
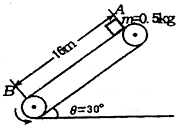如图所示，传递带与水平面的夹角θ=30°，A、B间传递带长16m传送带以lOm/s的速率逆时针匀速转动，在传送带顶端A无初速释放一个质量为0.5kg的物体，它传送带之间的动摩擦因数为
之间的滑动摩擦因数为μ=0.5，传送带A端到B端的距离S=16m，则小物体从A端运动到B端所需的时间可能是多少？（g=10m/s2）