题目内容

5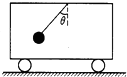．如图所示，在小车中悬挂一个小球，当小车沿平直路面做匀变速直线运动时，悬线偏离竖直方向的夹角为θ，此时小球相对小车静止，求小车加速度的大小．

分析 小球和小车具有相同的加速度，隔离对小球分析，根据牛顿第二定律求出加速度的大小．

解答 车厢的加速度与小球加速度相同，对小球进行受力分析，根据牛顿第二定律得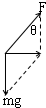
a=$\frac{{F}_{合}}{m}=\frac{mgtanθ}{m}$=gtanθ．
答：小车加速度的大小为gtanθ．

点评 本题主要考查了牛顿第二定律及力的合成与分解原则，要求同学们能正确对小球进行受力分析，基础题．

练习册系列答案
相关题目
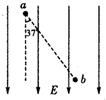17．如图所示，a，b是匀强电场中的两点，已知两点间的距离为0.4m．两点的连线与电场线成17°角．两点间的电势差为2.4×103V，则匀强电场的场强大小为E=7.5×103v/m，把电子从a点移到b点，电子的电势能将增加3.84×10-16J．（sin37°=0.6，cos37°=0.8，电子电量e=1.6×10-19C）
18．一雨滴从5m高的屋檐下落到地面所用的时间是1s，雨滴的下落运动是匀加速直线运动，则雨滴落地时的速度大小为10m/s，下落过程中加速度的大小是10m/s2．
13．如图所示，一质量m=0.4kg的小物块，以v0=2m/s的初速度，在与斜面成某一夹角的拉力F作用下，沿粗糙斜面上做匀速运动，经t=2s的时间物块由A点运动到B点，到达B点的速度8m/s，已知斜面倾角θ=30°，重力加速度g取10m/s2．
（1）求物块加速度的大小及A、B间的距离？
（2）拉力F与水平面夹角为60°时，若所用拉力最小值为$\frac{13\sqrt{3}}{5}$．求动摩擦因数为多大？
20．从匀减速上升的气球上释放一物体，在释放的瞬间，物体相对地面将具有（　　）
A．速度为零B．向下的速度C．向上的速度D．向上的加速度
10．现有两相同的某型号多用表，一同学在研究性学习过程中想获得10V量程直流电压档的内阻和×lk欧姆档的内部电源的电动势，已知×lk欧姆档中央刻度线对应的数据为15．为完成实验，进行了如下操作：
（1）将甲多用表档位旋钮拨到10V电压档，将乙多用表档位旋钮拨到×lk欧姆档；
（2）应将甲多用表的红表笔与乙多用表的黑（填“红”或“黑”）表笔连接，在将另外两表笔连接；
（3）在连接两多用表表笔之前应对乙多用表进行的操作为两表笔短接进行欧姆调零：
（4）两多用表连接后，两表读数分别为6.0V和30kΩ，可知10V量程直流电压档的内阻为30kΩ，×1k欧姆档的内部电源的电动势为9V．
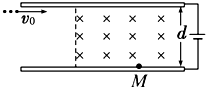17．如图所示，两块水平放置、相距为d的长金属板接在电压可调的电源上．两板之间的右侧区域存在方向垂直纸面向里的匀强磁场．将喷墨打印机的喷口靠近上板下表面，从喷口连续不断喷出质量均为m、水平速度均为v0、带相等电荷量的墨滴．调节电源电压至U，墨滴在电场区域恰能沿水平方向向右做匀速直线运动；进入电场、磁场共存区域后，最终垂直打在下板的M点．
（1）求其电荷量和磁感应强度B的值；
（2）现保持喷口方向不变，使其竖直下移到两板中间的位置．为了使墨滴仍能到达下板M点，应将磁感应强度调至B′，则B′的大小为多少？
14．如图所示，水平传送带以v=5m/s的恒定速度运动，传送带长AB=7.5m，今在其左端将一质量1kg工件轻轻放在上面，工件被带动，传送到右端，已知工件与传送带间的动摩擦因数μ=0.5，试求
（1）工件经过多少时间由传送带左端运动到右端？
（2）整个过程摩擦生热是多少？
15．如图所示，倾斜放置的平行板电容器两极板与水平面夹角θ，极板间距为d，带负电的微辟质量为m、带电量为q，从极板M的左边缘A处以初速度v0水平射入，沿直线运动并从极板N的右边缘B处射出，则（　　）
A．微粒达到B点时动能$\frac{1}{2}m{v}_{0}^{2}$B．微粒的加速度大小等gsinθ
C．两极板的电势${U}_{MN}=\frac{mgd}{qcosθ}$D．微粒从A点到B点的过程电势能减少

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网