题目内容
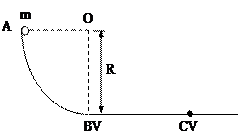
如图所示,在倾角为θ = 30o 的光滑斜面的底端有一个固定挡板D,小物体C靠在挡板D上,小物体B与C用轻质弹簧拴接。当弹簧处于自然长度时,B在O点;当B静止时,B在M点,OM = l。在P点还有一小物体A,使A从静止开始下滑,A、B相碰后一起压缩弹簧。A第一次脱离B后最高能上升到N点,ON =" 1.5" l。B运动还会拉伸弹簧,使C物体刚好能脱离挡板D。A、B、 C的质量都是m,重力加速度为g。求
C的质量都是m,重力加速度为g。求
(1)弹簧的劲度系数;
(2)弹簧第一次恢复到原长时B速度的大小;
(3)M、P之间的距离。
 C的质量都是m,重力加速度为g。求
C的质量都是m,重力加速度为g。求(1)弹簧的劲度系数;
(2)弹簧第一次恢复到原长时B速度的大小;
(3)M、P之间的距离。

(1)k=
(2)
(3)x=9l

(2)

(3)x=9l
(1)B静止时,弹簧形变量为l,弹簧产生弹力F=kl
B物体受力如图所示,根据物体平衡条件得
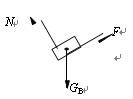
kl =mgsinθ (1分)
得弹簧的劲度系数k=
 (1分)
(1分)(2)当弹簧第一次恢复原长时A、B恰好分离,设此时A、B速度的大小为v3.(1分)
对A物体,从A、B分离到A速度变为0的过程,根据机械能守恒定律得
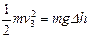 (1分)
(1分)此过程中A物体上升的高度
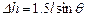
得
 (1分)
(1分)(3)设A与B相碰前速度的大小为v1,A与B相碰后速度的大小为v2,M、P之间距离为x.对A物体,从开始下滑到A、B相碰的过程,根据机械能守恒定律得
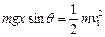 (1分)
(1分)A与B发生碰撞,根据动量守恒定律得 m v1=(m+m)v2 (1分)
设B静止时弹簧的弹性势能为EP,从A、B开始压缩弹簧到弹簧第一次恢复原长的过程,根据机械能守恒定律得
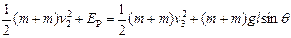 (1分)
(1分)B物体的速度变为0时,C物体恰好离开挡板D,此时弹簧的伸长量也为l,弹簧的弹性势能也为EP.对B物体和弹簧,从A、B分离到B速度变为0的过程,根据机械能守恒定律得
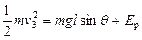 (1分)
(1分)解得 x=9l (1分)

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
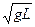 ?
?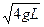 ?
?