题目内容
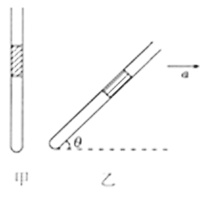
【题目】如图所示,在光滑水平面上有一个质量为m的水平凹槽,凹槽内右端放一个质量为m/n的物块(可视为质点)。t=0时刻,凹槽获得向右的初速度v0,同时物块获得向左的初速度nv0,物块与凹槽碰撞时间极短且为弹性碰撞。已知凹槽与物块之间的动摩擦因数为μ,凹槽长度为,重力加速度为g。求:

(1)物块最终的速度;
(2)若取n=2,求:从t=0时刻开始到与凹槽相对静止,物块的位移大小和方向;
(3)若取n=1,求:①从t=0时刻开始,经过多长时间系统的机械能损失36%;
②从t=0时刻开始到与凹槽相对静止,物块通过的总路程。
【答案】(1)0 (2)![]() ,方向水平向左 (3)①
,方向水平向左 (3)①![]() ;②
;②![]()
【解析】
(1)设物块和凹槽最终相对静止时对地的速度为v,系统动量守恒:![]()
解得v=0
(2)在整个运动的过程中,系统的动量恒定为零,即两物体动量大小时刻相等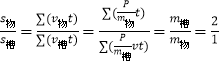
设物块在凹槽内划过的相对路程为s,由能量守恒可得:![]()
解得![]() 是凹槽长度的4.4倍,所以物块在凹槽发生的相对位移等于0.4倍的槽长,即
是凹槽长度的4.4倍,所以物块在凹槽发生的相对位移等于0.4倍的槽长,即![]()
即:![]()
解得![]() 方向水平向左;
方向水平向左;
(3)①两物块碰撞时互换速度,系统机械能损失36%时,此时两物体速度等大反向,设为v1,满足![]()
解得![]()
两物体的加速度大小相等,且恒定为![]()
取向右为正向,建立v-t图像;当
速度为![]() 时,经历的时间为
时,经历的时间为![]()
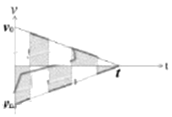
②由v-t图像可知;物块最终通过的路程为阴影部分的面积和:![]()

练习册系列答案
相关题目