题目内容
如图所示,两根平行金属导轨MN,PQ相距为d =1.0m,导轨平面与水平面夹角为a=300导轨上端跨接一定值电阻R=1.6Ω,导轨电阻不计。整个装置处于方向垂直导轨平面向上、磁感应强度大小B=1T的匀强磁场中。金属棒ef垂直于MN、PQ静止放置,且与导轨保持良好接触,其长刚好也为d、质量m=0.1kg、电阻r=0.4Ω,距导轨底端s1=3.75m另一根与金属棒平行放置的绝缘棒gh长度也为d,质量为 ,从轨道最低点以速度v0=10m/s沿轨道上滑并与金属棒发生正碰(碰撞时间极短),碰后金属棒沿导轨上滑s2=0.2m后再次静止,测得此过程中电阻R上产生的电热为Q=0.2J己知两棒与导轨间的动摩擦因数均为.
,从轨道最低点以速度v0=10m/s沿轨道上滑并与金属棒发生正碰(碰撞时间极短),碰后金属棒沿导轨上滑s2=0.2m后再次静止,测得此过程中电阻R上产生的电热为Q=0.2J己知两棒与导轨间的动摩擦因数均为. ,g取10m/s2,求:
,g取10m/s2,求:

(1) 碰后瞬问两棒的速度;
(2) 碰后瞬间金属棒的加速度;
(3) 金属棒在导轨上运动的时间。
 ,从轨道最低点以速度v0=10m/s沿轨道上滑并与金属棒发生正碰(碰撞时间极短),碰后金属棒沿导轨上滑s2=0.2m后再次静止,测得此过程中电阻R上产生的电热为Q=0.2J己知两棒与导轨间的动摩擦因数均为.
,从轨道最低点以速度v0=10m/s沿轨道上滑并与金属棒发生正碰(碰撞时间极短),碰后金属棒沿导轨上滑s2=0.2m后再次静止,测得此过程中电阻R上产生的电热为Q=0.2J己知两棒与导轨间的动摩擦因数均为. ,g取10m/s2,求:
,g取10m/s2,求:
(1) 碰后瞬问两棒的速度;
(2) 碰后瞬间金属棒的加速度;
(3) 金属棒在导轨上运动的时间。
解:(1)设金属棒碰后的速度为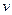 ,
,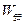 为金属棒克服安培力做的功
为金属棒克服安培力做的功
对金属棒碰后的过程,由动能定理:
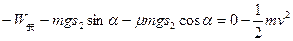 ① (2分)
① (2分)
再由功能关系,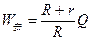 ② (2分)
② (2分)
得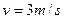
 (1分)
(1分)
设绝缘棒与金属棒碰前的速度为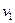 ,对绝缘棒在导轨上滑动过程,由动能定理
,对绝缘棒在导轨上滑动过程,由动能定理
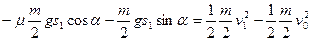 ③ (2分)
③ (2分)
得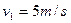 (1分)
(1分)
设绝缘棒碰后的速度为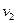 ,选沿导轨向上的方向为正方向,
,选沿导轨向上的方向为正方向,
两棒碰撞过程,由动量守恒定律: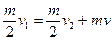 ④ (2分)
④ (2分)
得 m/s,负号表示方向沿导轨向下 (1分)
m/s,负号表示方向沿导轨向下 (1分)
(2) 碰后金属棒切割磁感线产生的感应电动势为 ,
,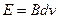 ⑤ (1分)
⑤ (1分)
回路中的感应电流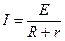 ⑥ (1分)
⑥ (1分)
安培力的大小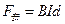 ⑦ (1分)
⑦ (1分)
设金属棒的加速度为a,对金属棒,由牛顿第二定律:
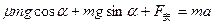 ⑧ (1分)
⑧ (1分)
联立⑤⑥⑦⑧解出: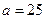 m/s2,方向沿导轨平面向下 (1分)
m/s2,方向沿导轨平面向下 (1分)
(3) 设金属棒在导轨上运动时间为t,在此运动过程中,安培力的冲量大小为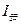 ,沿导轨方向由动量定理:
,沿导轨方向由动量定理: 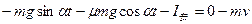 ⑨ (2分)
⑨ (2分)
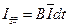 ⑩ (1分)
⑩ (1分)
由闭合电路欧姆定律: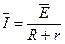
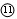 (1分)
(1分)
由法拉第电磁感应定律: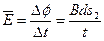
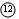 (1分)
(1分)
联立⑨⑩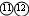 解得:
解得: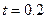 s (1分)
s (1分)
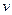 ,
,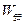 为金属棒克服安培力做的功
为金属棒克服安培力做的功对金属棒碰后的过程,由动能定理:
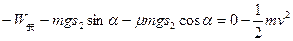 ① (2分)
① (2分)再由功能关系,
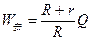 ② (2分)
② (2分)得
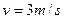
 (1分)
(1分)设绝缘棒与金属棒碰前的速度为
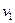 ,对绝缘棒在导轨上滑动过程,由动能定理
,对绝缘棒在导轨上滑动过程,由动能定理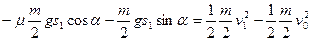 ③ (2分)
③ (2分)得
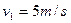 (1分)
(1分)设绝缘棒碰后的速度为
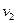 ,选沿导轨向上的方向为正方向,
,选沿导轨向上的方向为正方向,两棒碰撞过程,由动量守恒定律:
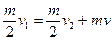 ④ (2分)
④ (2分)得
 m/s,负号表示方向沿导轨向下 (1分)
m/s,负号表示方向沿导轨向下 (1分)(2) 碰后金属棒切割磁感线产生的感应电动势为
 ,
,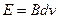 ⑤ (1分)
⑤ (1分)回路中的感应电流
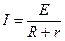 ⑥ (1分)
⑥ (1分)安培力的大小
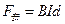 ⑦ (1分)
⑦ (1分)设金属棒的加速度为a,对金属棒,由牛顿第二定律:
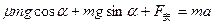 ⑧ (1分)
⑧ (1分)联立⑤⑥⑦⑧解出:
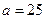 m/s2,方向沿导轨平面向下 (1分)
m/s2,方向沿导轨平面向下 (1分)(3) 设金属棒在导轨上运动时间为t,在此运动过程中,安培力的冲量大小为
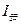 ,沿导轨方向由动量定理:
,沿导轨方向由动量定理: 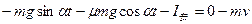 ⑨ (2分)
⑨ (2分)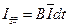 ⑩ (1分)
⑩ (1分) 由闭合电路欧姆定律:
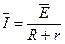
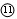 (1分)
(1分)由法拉第电磁感应定律:
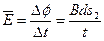
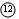 (1分)
(1分)联立⑨⑩
 解得:
解得: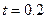 s (1分)
s (1分)略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



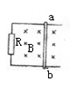
 圈A是通过高频交流电的线圈,B是自行车的零件,a是待焊接的接口,焊口两端接触在一起。当A中通有交变电流时,B中会产生感应电流,使得接口处的金属融化而焊接起来
圈A是通过高频交流电的线圈,B是自行车的零件,a是待焊接的接口,焊口两端接触在一起。当A中通有交变电流时,B中会产生感应电流,使得接口处的金属融化而焊接起来