��Ŀ����
12��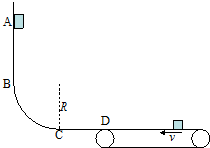 ��ͼ��ʾ���⻬���ABCD��BCΪ$\frac{1}{4}$Բ����Բ���뾶ΪR��CD����ˮƽ��ĩ��D�����Ҷ��㹻����ˮƽ���ʹ������ӣ����ʹ��Ժ㶨�ٶ�v��ʱ��ת�����ֽ�һ����Ϊm��С����ӹ����A���ɾ�ֹ�ͷţ�A��C����ֱ�߶�ΪH��������
��ͼ��ʾ���⻬���ABCD��BCΪ$\frac{1}{4}$Բ����Բ���뾶ΪR��CD����ˮƽ��ĩ��D�����Ҷ��㹻����ˮƽ���ʹ������ӣ����ʹ��Ժ㶨�ٶ�v��ʱ��ת�����ֽ�һ����Ϊm��С����ӹ����A���ɾ�ֹ�ͷţ�A��C����ֱ�߶�ΪH��������| A�� | �����ڴ������������˶����������봫�����ٶ�v�� | |
| B�� | С���鲻���ܷ���A�� | |
| C�� | ��H=4R�����龭��C��ʱ�Թ��ѹ����СΪ8mg | |
| D�� | ��H=4R��Ƥ���ٶ�v��=$\sqrt{2gR}$��������һ�λ��ϴ�����������Ħ��������������Ϊ9mgR |
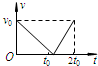
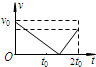
���� �����ڴ��ʹ����ܵ������Ħ������������ǡ���ٶȵ���0ʱ�������˶��ľ�������ݶ��ܶ���������ý����
�����ڴ��ʹ����˶�ʱ��ˮƽ����ֻ�ܵ�Ħ���������ã�����ţ�ٵڶ�������ü��ٶȣ�Ȼ����λ�ƹ�ʽ���ٶȹ�ʽ����������λ�ƣ�����Q=Ffl������������
��� �⣺A�����ڴ��ʹ���ʱ�뷽���˶�����֪�����������˶��Ĺ�����һֱ�������˶���������ǡ���ٶȵ���0ʱ�������˶��ľ�����þ����봫�ʹ����ٶ��أ���A��ȷ��
B�������ڴ��ʹ��������Ҽ��٣�Ȼ���ڴ��ʹ��������������˶���������ʹ����ٶ��㹻��������һֱ�������˶�ʱ�����˶��ĶԳ��Կ�֪�������뿪���ʹ����ٶ��뻬�ϴ��ʹ����ٶȴ�С��ȣ����ԴﵽA�㣮��B����
C����H=4R�����龭��C��ʱ���ٶȣ�$v=\sqrt{2gH}=\sqrt{2g��4R}=2\sqrt{2gR}$
�����ܵ���֧�����������ĺ����ṩ�����������ԣ�${F}_{N}-mg=\frac{m{v}^{2}}{R}$
�ã�FN=9mg
����ţ�ٵ������ɿ�֪������Թ��ѹ����СΪ9mg����C����
D��ѡ������Ϊ�������軬���봫�ʹ�֮��Ķ�Ħ�������Ǧ̣���ļ��ٶȣ�$a=\frac{-��mg}{m}=-��g$
������ٶ�Ϊ-$\sqrt{2gR}$ʱ��ʹ�õ�ʱ�䣺
$t=\frac{��v}{a}=\frac{��v}{-��g}=\frac{-\sqrt{2gR}-2\sqrt{2gR}}{-��g}$=$\frac{3\sqrt{2gR}}{��g}$
�����λ�ƣ�${x}_{1}=vt+\frac{1}{2}a{t}^{2}$
�������ݵã�${x}_{1}=\frac{3R}{��}$
���ʱ���ڴ��ʹ���λ�ƣ�${x}_{2}=v��t=-\sqrt{2gR}•\frac{3\sqrt{2gR}}{��g}=-\frac{6R}{��}$
�����봫�ʹ�֮������λ�ƣ�$��x={x}_{1}-{x}_{2}=\frac{3R}{��}-��-\frac{6R}{��}��=\frac{9R}{��}$
����Ħ��������������Ϊ��Q=f��x=$��mg•\frac{9R}{��}$=9mgR��D��ȷ��
��ѡ��AD
���� �����ۺϿ����˶��ܶ�������е���غ㶨�ɺ�ţ�ٵڶ����ɣ��������Ĺؼ�����������˶����̣�֪��������˶����ɣ���϶��ܶ�����ţ�ٵڶ����ɺ��˶�ѧ��ʽ������⣮

 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�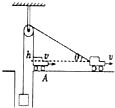 ��ͼ��ʾ��ijС����һ����Ϊm������Ӿ��������������������ӵ��ֶ����Ϊh����ʼʱ���徲ֹ��A�㣬�һ��������������ֱ�������������ٶ�vˮƽ��������ֱ���˶��������������ӵ�ϸ��ˮƽ����ļн�Ϊ60�㣬������һ��Ħ����������
��ͼ��ʾ��ijС����һ����Ϊm������Ӿ��������������������ӵ��ֶ����Ϊh����ʼʱ���徲ֹ��A�㣬�һ��������������ֱ�������������ٶ�vˮƽ��������ֱ���˶��������������ӵ�ϸ��ˮƽ����ļн�Ϊ60�㣬������һ��Ħ����������| A�� | ���˶������У�����mһֱ�������˶� | |
| B�� | �˶������У�ϸ����������������ǵ���mg | |
| C�� | ������ˮƽ����ļн�Ϊ60��ʱ������m�������ٶ�Ϊ$\frac{v}{2}$ | |
| D�� | ������ˮƽ����ļн�Ϊ60��ʱ���������ʵ���$\frac{1}{2}$mgv |
| A�� | ���Ӽ��Խ������ԽС����������Խ�� | |
| B�� | �����˶����ܷ�ӳҺ����ӵ����˶� | |
| C�� | ��������ԭ�ӣ�����ӡ����ӣ� �����ж����пռ��ϵ������� | |
| D�� | ��Һ���еĵ糡ǿ�Ȳ�ͬʱ��Һ����ʾ��������ʾ������ɫ |
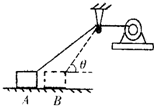 ��ͼ��ʾ��ij������ͷ���綯���Ժ㶨�Ĺ���P�ͺ㶨��ת��n�������ӣ���������ΪM�ļ�װ����ˮƽ��������A�˶���B�����綯���������ӵ����Ӱ뾶ΪR����װ����ˮƽ��Ħ�����ƣ�����˵����ȷ���ǣ�������
��ͼ��ʾ��ij������ͷ���綯���Ժ㶨�Ĺ���P�ͺ㶨��ת��n�������ӣ���������ΪM�ļ�װ����ˮƽ��������A�˶���B�����綯���������ӵ����Ӱ뾶ΪR����װ����ˮƽ��Ħ�����ƣ�����˵����ȷ���ǣ�������| A�� | ���˶���������ˮƽ��ɦȽ�ʱ����װ���ٶ���2��nRcos�� | |
| B�� | ���˶���������ˮƽ��ɦȽ�ʱ����װ��Եص�ѹ��Ϊ��Mg-$\frac{Psin��}{2��nR}$�� | |
| C�� | ��A��B�����������ϵ�������С���䣬���СΪ$\frac{P}{2��nR}$ | |
| D�� | ��A��B�����м�װ�����ܺ����Ĵ�С�ͷ����ڱ仯 |
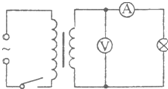 ��ͼ��ʾ�������ѹ��ԭ��Ȧ�����е��ѹ��220V��50Hz�����պϵ����������ʾ��ΪO��10A����ѹ����ʾ��Ϊ22V���ɴ˿�֪�ñ�ѹ���ģ�������
��ͼ��ʾ�������ѹ��ԭ��Ȧ�����е��ѹ��220V��50Hz�����պϵ����������ʾ��ΪO��10A����ѹ����ʾ��Ϊ22V���ɴ˿�֪�ñ�ѹ���ģ�������| A�� | ԭ������Ȧ��������Ϊ1��10 | B�� | ԭ������Ȧ��������Ϊ10��1 | ||
| C�� | ԭ��Ȧ����Ϊ0.01A | D�� | ����Ȧ�������Ƶ��Ϊ5Hz |


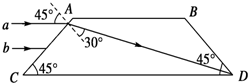 ��ͼ��ʾ����ƽ�в���ש�Ľ���ͼ��һ��ƽ����CD�ߵĵ�ɫ�����䵽AC�����ϣ�a��b�����е�����ƽ�й��ߣ�����a�ڲ���ש�еĹ�·�Ѹ�������������b�Ӳ���ש���״γ���Ĺ�·ͼ������������������淨�нǵĶ�����ע�⣺�����ø����ͼ���ǶȾ���ȷ��
��ͼ��ʾ����ƽ�в���ש�Ľ���ͼ��һ��ƽ����CD�ߵĵ�ɫ�����䵽AC�����ϣ�a��b�����е�����ƽ�й��ߣ�����a�ڲ���ש�еĹ�·�Ѹ�������������b�Ӳ���ש���״γ���Ĺ�·ͼ������������������淨�нǵĶ�����ע�⣺�����ø����ͼ���ǶȾ���ȷ��