题目内容
16. 在倾斜角为θ的长斜面上,一带有风帆的滑块从静止开始沿斜面下滑,滑块(连同风帆)的质量为m,滑块与斜面间的动摩擦因数为μ,风帆受到的空气阻力与滑块下滑的速度v大小成正比,即f=kv(k未知),方向与v 的方向相反.滑块从静止开始沿斜面下滑的v-t图象如图所示,图中的倾斜直线是t=0时刻速度图线的切线.求:
在倾斜角为θ的长斜面上,一带有风帆的滑块从静止开始沿斜面下滑,滑块(连同风帆)的质量为m,滑块与斜面间的动摩擦因数为μ,风帆受到的空气阻力与滑块下滑的速度v大小成正比,即f=kv(k未知),方向与v 的方向相反.滑块从静止开始沿斜面下滑的v-t图象如图所示,图中的倾斜直线是t=0时刻速度图线的切线.求:(1)滑块运动的最大速度和最大加速度
(2)k值的大小.
分析 根据图象得出滑块的最大速度,根据图线的斜率得出最大加速度.
对t=0时刻运用牛顿第二定律列出表达式,对滑块达到最大速度时列出平衡的表达式,联立求出k值的大小.
解答 解:(1)由图象知:滑块的最大速度vm=2m/s,
t=0时,加速度a最大,${a}_{m}=\frac{△v}{△t}=\frac{3}{1}m/{s}^{2}=3m/{s}^{2}$.
(2)根据牛顿第二定律得mgsin37°-μmgcos37°=mam,
解得$μ=\frac{gsin37°-{a}_{m}}{gcos37°}=0.375$.
达最大速度后,滑块做匀速直线运动,有:
mgsin37°=μmgcos37°+kvm,
解得$k=\frac{mg(sin37°-μcos37°)}{{v}_{m}}$=3N.s/m.
答:(1)滑块运动的最大速度为2m/s,最大加速度为3m/s2;
(2)k值的大小为3N.s/m.
点评 本题考查了牛顿第二定律、共点力平衡与速度时间图线的综合,知道图线的斜率表示加速度,结合牛顿第二定律和共点力平衡进行求解.

练习册系列答案
相关题目
17.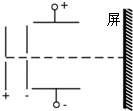 如图所示,氕核、氘核、氚核三种粒子从同一位置无初速地飘入电场线水平向右的加速电场E1,之后进入电场线竖直向下的匀强电场E2发生偏转,最后打在屏上.整个装置处于真空中,不计粒子重力及其相互作用,那么( )
如图所示,氕核、氘核、氚核三种粒子从同一位置无初速地飘入电场线水平向右的加速电场E1,之后进入电场线竖直向下的匀强电场E2发生偏转,最后打在屏上.整个装置处于真空中,不计粒子重力及其相互作用,那么( )
 如图所示,氕核、氘核、氚核三种粒子从同一位置无初速地飘入电场线水平向右的加速电场E1,之后进入电场线竖直向下的匀强电场E2发生偏转,最后打在屏上.整个装置处于真空中,不计粒子重力及其相互作用,那么( )
如图所示,氕核、氘核、氚核三种粒子从同一位置无初速地飘入电场线水平向右的加速电场E1,之后进入电场线竖直向下的匀强电场E2发生偏转,最后打在屏上.整个装置处于真空中,不计粒子重力及其相互作用,那么( )| A. | 偏转电场E2对三种粒子做功一样多 | B. | 三种粒子打到屏上时的速度一样大 | ||
| C. | 三种粒子运动到屏上所用时间相同 | D. | 三种粒子一定打到屏上的同一位置 |
18.过去几千年来,人类对行星的认识与研究仅限于太阳系内,行星“51 peg b”的发现拉开了研究太阳系外行星的序幕,“51 peg b”绕其中心恒星做匀速圆周运动,周期约为4天,轨道半径约为地球绕太阳运动半径的$\frac{1}{20}$,该中心恒星与太阳的质量比约为( )
| A. | $\frac{1}{10}$ | B. | 1 | C. | 5 | D. | 10 |
4.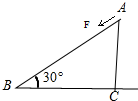 如图所示,水平面上固定有高为AC=H、倾角为30°的直角三角形光滑斜面,有一长为2H、质量为m的均匀绳,其一端拴有质量为m(可看作质点)的小球,另一端在外力F作用下通过斜面顶端的光滑小定滑轮从A点沿斜面缓慢运动到B点,不计绳绷紧是的能量损失,则该过程中( )
如图所示,水平面上固定有高为AC=H、倾角为30°的直角三角形光滑斜面,有一长为2H、质量为m的均匀绳,其一端拴有质量为m(可看作质点)的小球,另一端在外力F作用下通过斜面顶端的光滑小定滑轮从A点沿斜面缓慢运动到B点,不计绳绷紧是的能量损失,则该过程中( )
 如图所示,水平面上固定有高为AC=H、倾角为30°的直角三角形光滑斜面,有一长为2H、质量为m的均匀绳,其一端拴有质量为m(可看作质点)的小球,另一端在外力F作用下通过斜面顶端的光滑小定滑轮从A点沿斜面缓慢运动到B点,不计绳绷紧是的能量损失,则该过程中( )
如图所示,水平面上固定有高为AC=H、倾角为30°的直角三角形光滑斜面,有一长为2H、质量为m的均匀绳,其一端拴有质量为m(可看作质点)的小球,另一端在外力F作用下通过斜面顶端的光滑小定滑轮从A点沿斜面缓慢运动到B点,不计绳绷紧是的能量损失,则该过程中( )| A. | 绳子的重力做功为0 | B. | 绳的重力势能增加了$\frac{1}{4}$mgH | ||
| C. | 绳的机械能增加了$\frac{1}{4}$mgH | D. | 小球对绳的拉力做功mgH |
11. 如图为某探究活动小组设计的节能运输系统的简化示意图.斜面轨道倾角为37°,质量为M的货箱与轨道的动摩擦因数为0.5.货箱在轨道顶端时,自动装货装置将质量为m的货物装入货箱,然后货箱载着货物沿轨道无初速滑下,当轻弹簧压缩至最短时,自动卸货装置立刻将货物卸下,然后货箱恰好被弹回到轨道顶端,再重复上述过程.已知sin37°=0.6,cos37°=0.8,下列选项正确的是( )
如图为某探究活动小组设计的节能运输系统的简化示意图.斜面轨道倾角为37°,质量为M的货箱与轨道的动摩擦因数为0.5.货箱在轨道顶端时,自动装货装置将质量为m的货物装入货箱,然后货箱载着货物沿轨道无初速滑下,当轻弹簧压缩至最短时,自动卸货装置立刻将货物卸下,然后货箱恰好被弹回到轨道顶端,再重复上述过程.已知sin37°=0.6,cos37°=0.8,下列选项正确的是( )
 如图为某探究活动小组设计的节能运输系统的简化示意图.斜面轨道倾角为37°,质量为M的货箱与轨道的动摩擦因数为0.5.货箱在轨道顶端时,自动装货装置将质量为m的货物装入货箱,然后货箱载着货物沿轨道无初速滑下,当轻弹簧压缩至最短时,自动卸货装置立刻将货物卸下,然后货箱恰好被弹回到轨道顶端,再重复上述过程.已知sin37°=0.6,cos37°=0.8,下列选项正确的是( )
如图为某探究活动小组设计的节能运输系统的简化示意图.斜面轨道倾角为37°,质量为M的货箱与轨道的动摩擦因数为0.5.货箱在轨道顶端时,自动装货装置将质量为m的货物装入货箱,然后货箱载着货物沿轨道无初速滑下,当轻弹簧压缩至最短时,自动卸货装置立刻将货物卸下,然后货箱恰好被弹回到轨道顶端,再重复上述过程.已知sin37°=0.6,cos37°=0.8,下列选项正确的是( )| A. | 货箱载着货物接触弹簧时立即开始减速运动 | |
| B. | 货物质量m应为货箱质量M的4倍 | |
| C. | 货箱不与弹簧接触时,上滑的加速度大于下滑的加速度 | |
| D. | 货箱从最低点滑回顶端的过程中,弹簧的弹性势能全部转化为货箱的重力势能 |
8.电磁灶是利用电磁感应原理加热的一种新型灶具,下列对电磁灶的相关说法中正确的是( )
| A. | 加热用锅体其材料可采用陶瓷 | |
| B. | 锅体中的涡流是由恒定的磁场产生的 | |
| C. | 锅体中的涡流是由变化的磁场产生的 | |
| D. | 提高磁场变化的频率,可提高电磁灶的加热效果 |
 如图所示,上表面水平的平板车B右端固定一轻质弹簧,平板车左端与弹簧的自由端相距L,开始时静止在光滑水平面上,在平板车最左端静止放置一小物块A,一颗质量为m0的子弹以水平初速度v0迅速射穿A后,速度变为$\frac{{v}_{0}}{2}$,子弹射穿前后物块A的质量不变.此后,物块A向右运动压缩弹簧后被弹回并停在小车最左端(弹簧始终在弹性限度内),已知平板车B质量为10m0,物块A质量为2m0.A、B之间的动摩擦因数为μ,重力加速度为g.求:
如图所示,上表面水平的平板车B右端固定一轻质弹簧,平板车左端与弹簧的自由端相距L,开始时静止在光滑水平面上,在平板车最左端静止放置一小物块A,一颗质量为m0的子弹以水平初速度v0迅速射穿A后,速度变为$\frac{{v}_{0}}{2}$,子弹射穿前后物块A的质量不变.此后,物块A向右运动压缩弹簧后被弹回并停在小车最左端(弹簧始终在弹性限度内),已知平板车B质量为10m0,物块A质量为2m0.A、B之间的动摩擦因数为μ,重力加速度为g.求: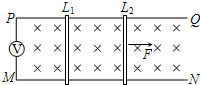 如图所示,固定于水平桌面上足够长的两平行导轨PQ、MN,PQ、MN的电阻不计,间距为d=0.5m.P、M两端接有一只理想电压表,整个装置处于竖直向下的磁感应强度B=0.2T的匀强磁场中.电阻分别为R1=0.4Ω、R2=0.1Ω、质量分别为m1=0.3kg和m2=0.5kg的两金属棒L1、L2平行的搁在光滑导轨上.现固定棒L1,L2在水平恒力F=0.4N的作用下,由静止开始做加速运动,求:
如图所示,固定于水平桌面上足够长的两平行导轨PQ、MN,PQ、MN的电阻不计,间距为d=0.5m.P、M两端接有一只理想电压表,整个装置处于竖直向下的磁感应强度B=0.2T的匀强磁场中.电阻分别为R1=0.4Ω、R2=0.1Ω、质量分别为m1=0.3kg和m2=0.5kg的两金属棒L1、L2平行的搁在光滑导轨上.现固定棒L1,L2在水平恒力F=0.4N的作用下,由静止开始做加速运动,求: