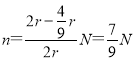Question

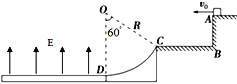
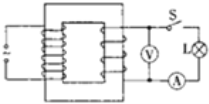
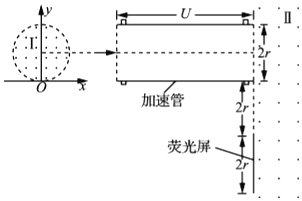
【题目】如图所示，半径为r的圆形匀强磁场区域I与x轴相切与坐标系的原点O，磁感应强度为B1，方向垂直于纸面向外，磁场区域I右侧有一长方体加速管，加速管底面宽度为2r，轴线与x轴平行且过磁场区域I的圆心，左侧的电势比右侧高U．在加速管出口下侧距离2r处放置一宽度为2r的荧光屏，加速管右侧存在方向垂直于纸面向外的匀强磁场区域II，在O点处有一个粒子源，能沿纸面向y＞0的各个方向均匀地发射大量质量为m、带电荷量为q且速率相同的粒子，其中沿y轴正方向射入磁场的粒子，恰能沿轴线进入长方形加速管并打在荧光屏的中心位置，（不计粒子重力及其相互作用）

（1）求粒子刚进入加速管时的速度大小；

（2）求磁场区域II的磁感应强度大小B2；

（3）若进入加速管的粒子数目为N，则磁场II的磁感应强度B2减小10%时，有多少离子能打在荧光屏上．

Answer 1

【答案】(1) (2) (3)

【解析】（1）沿y轴正方向射入磁场的粒子，恰能沿轴线进入长方形加速管并打在荧光屏的中心位置，则磁场区域I内粒子运动轨迹半径距离为r，在匀强磁场Ⅰ中粒子做圆周运动，洛伦兹力作向心力，则有：B1vq＝，
解得： ；
（2）沿y轴正方向射入磁场的粒子，恰能沿轴线进入长方形加速管，则由动能定理可得粒子进入磁场Ⅱ的速度为v′，有关系式：Uq＝mv′2mv2；
解得： ；
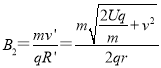因为粒子在磁场Ⅱ中运动，并打在荧光屏的中心位置，所以，粒子在磁场Ⅱ中做圆周运动的半径R′=2r，由洛伦兹力作向心力可得：B2v′q＝，所以， ，其中；
（3）在匀强磁场Ⅰ中，设粒子从P点离开磁场，如图所示，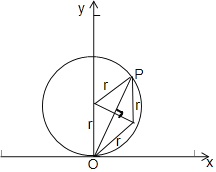
，
因为粒子做圆周运动的圆心在弦长的垂直平分线上，且磁场区域和圆周运动的半径都为r，所以，磁场区域的两条半径和圆周运动轨迹的两条半径构成菱形，所以，在P点的径向平行于y轴，所以，粒子离开磁场时的速度为水平方向．
若进入加速管的粒子数目为N，则这N个粒子在竖直方向上均匀分布；
在磁场中粒子做匀速圆周运动，洛伦兹力作向心力，有：Bvq＝，
解得： ；
磁场II的磁感应强度B2减小10%时，则粒子在磁场Ⅱ中做圆周运动的半径为： ，
设粒子进入磁场Ⅱ时，竖直高度为y，则只要：0≤2R″-2r-y≤2r，粒子就可以打在荧光屏上，
所以， r≤y≤r，因为N个粒子在0≤y≤2r上均匀分布，所以打在屏上的粒子数为：