题目内容
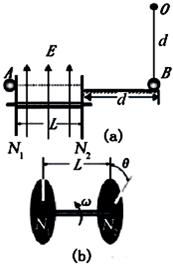
如图(a)所示,左侧为某课外活动小组设计的某种速度选择装置(图(b)为它的立体图),由水平转轴及两个薄盘N1、N2构成,两盘面平行且与转轴垂直,相距为L,两盘面间存在竖直向上的匀强电场,盘上各开一狭缝,两狭缝夹角可调;右侧为长为d的水平桌面,水平桌面的右端有一质量为m绝缘小球B,用长也为d的不可伸长的细线悬挂,B对水平桌面压力刚好为零.今有电荷量为q,质量也为m的另一带电小球A沿水平方向射入N1狭缝,匀速通过两盘间后通过N2的狭缝,并沿水平桌面运动到右端与小球B发生碰撞,设A与B碰撞时速度发生交换.已知小球A与水平桌面间动摩擦因数为μ,求:
(1)小球A带何种电及两盘面间的电场强度E的大小;
(2)若要求小球A能与小球B相撞,那么当小球A从N2中穿出时它的速度应满足什么条件;
(3)若两狭缝夹角调为θ,盘匀速转动,转动方向如图(b),要使小球A与小球B碰撞后,B恰好做完整的圆周运动,求薄盘转动的角速度ω.
(1)小球A带何种电及两盘面间的电场强度E的大小;
(2)若要求小球A能与小球B相撞,那么当小球A从N2中穿出时它的速度应满足什么条件;
(3)若两狭缝夹角调为θ,盘匀速转动,转动方向如图(b),要使小球A与小球B碰撞后,B恰好做完整的圆周运动,求薄盘转动的角速度ω.

(1)小球A匀速通过两盘过程电场力和重力平衡,小球A带正电.
且:mg=qE
得:E=
(2)设小球通过N2时的速度为v0,与小球B发生碰撞前瞬间的速度为vA,对小球A在水平桌面上的运动由动能定理得:
-μmgd=
m
-
m
A与B相撞须满足条件:vA>0
得:v0>
(3)小球B碰后恰好做完整的圆周运动有:mg=m
小球B从最低到最高点由动能定理有:-mg2d=
m
-
m
又由题,vA=vB
设小球A通过N2的速度为v,根据动能定理:-μmgd=
m
-
m
小球A能通过转盘有:
=
由以上各式得:ω=
(n=0,1,2,3…)
答:(1)小球A带正电,两盘面间的电场强度E的大小是
;
(2)若要求小球A能与小球B相撞,当小球A从N2中穿出时它的速度应满足的条件是:v0>
;
(3)若两狭缝夹角调为θ,要使小球A与小球B碰撞后,B恰好做完整的圆周运动,薄盘转动的角速度ω=
(n=0,1,2,3…).
且:mg=qE
得:E=
| mg |
| q |
(2)设小球通过N2时的速度为v0,与小球B发生碰撞前瞬间的速度为vA,对小球A在水平桌面上的运动由动能定理得:
-μmgd=
| 1 |
| 2 |
| v | 2A |
| 1 |
| 2 |
| v | 20 |
A与B相撞须满足条件:vA>0
得:v0>
| 2μgd |
(3)小球B碰后恰好做完整的圆周运动有:mg=m
| ||
| d |
小球B从最低到最高点由动能定理有:-mg2d=
| 1 |
| 2 |
| v | ′2B |
| 1 |
| 2 |
| v | 2B |
又由题,vA=vB
设小球A通过N2的速度为v,根据动能定理:-μmgd=
| 1 |
| 2 |
| v | 2A |
| 1 |
| 2 |
| v | 2 |
小球A能通过转盘有:
| L |
| v |
| 2nπ+θ |
| ω |
由以上各式得:ω=
| 2nπ+θ |
| L |
| 5gd+2μgd |
答:(1)小球A带正电,两盘面间的电场强度E的大小是
| mg |
| q |
(2)若要求小球A能与小球B相撞,当小球A从N2中穿出时它的速度应满足的条件是:v0>
| 2μgd |
(3)若两狭缝夹角调为θ,要使小球A与小球B碰撞后,B恰好做完整的圆周运动,薄盘转动的角速度ω=
| 2nπ+θ |
| L |
| 5gd+2μgd |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目