题目内容
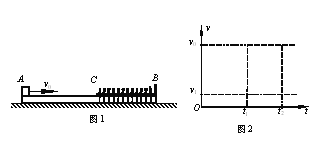
【题目】如图(a)所示,足够长的光滑平行金属导轨JK、PQ倾斜放置,两导轨间距离为L=l.0 m,导轨平面与水平面间的夹角为θ=30°,磁感应强度为B的匀强磁场垂直于导轨平面向上,导轨的J、P两端连接阻值为R=3.0Ω的电阻,金属棒ab垂直于导轨放置并用细线通过光滑定滑轮与重物相连,金属棒ab的质量m=0.20 kg,电阻r=0.50 Ω,重物的质量M=0.60 kg,如果将金属棒和重物由静止释放,金属棒沿斜面上滑距离与时间的关系图像如图(b)所示,不计导轨电阻, g=10 m/s 2 。求:
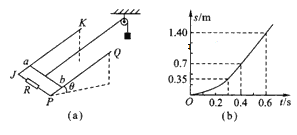
(1)t=0时刻金属棒的加速度
(2)求磁感应强度B的大小以及在0.6 s内通过电阻R的电荷量;
(3)在0.6 s内电阻R产生的热量。
【答案】(1)a=6.25m/s2 (2)![]() (3)QR=1.8J
(3)QR=1.8J
【解析】
根据电量公式q=I△t,闭合电路欧姆定律![]() ,法拉第电磁感应定律:
,法拉第电磁感应定律:![]() ,联立可得通过电阻R的电量;由能量守恒定律求电阻R中产生的热量。
,联立可得通过电阻R的电量;由能量守恒定律求电阻R中产生的热量。
(1) 对金属棒和重物整体
Mg-mgsinθ=(M+m)a
解得:a=6.25m/s2 ;
(2) 由题图(b)可以看出最终金属棒ab将匀速运动,匀速运动的速度
![]()
感应电动势E=BLv 感应电流![]()
金属棒所受安培力![]()
速运动时,金属棒受力平衡,则可得
![]()
联立解得:![]()
在0.6 s内金属棒ab上滑的距离s=1.40m
通过电阻R的电荷量
![]() ;
;
(3) 由能量守恒定律得
![]()
解得Q=2.1 J
又因为
![]()
联立解得:QR=1.8J。

【题目】在“测定金属丝的电阻率”实验中,待测金属丝接入电路部分的长度约为50cm。
(1)用螺旋测微器测量金属丝的直径,其中某一次测量结果如图1所示,其读数为_______mm。
(2)用伏安法测金属丝的电阻Rx。
实验所用器材为:电池组(电动势为3V,内阻约1Ω)、电流表(内阻约0.1Ω)、电压表(内阻约3kΩ)、滑动变阻器R(0~20Ω,额定电流2A)、开关、导线若干。
某小组同学利用以上器材正确连接好电路,进行实验测量,记录数据如下:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
U/V | 0 | 0.10 | 0.30 | 0.70 | 1.00 | 1.50 | 1.70 | 2.30 |
I/A | 0 | 0.020 | 0.060 | 0.160 | 0.220 | 0.340 | 0.460 | 0.520 |
由以上数据可知,他们测量Rx是采用图2中的_________图(选填“甲”或“乙”)。

(3)图3是测量Rx的实验器材实物图,图中已连接了部分导线,滑动变阻器的滑片P置于变阻器的左端。请根据图2所选的电路图,在图3中补充完成该组同学实验时实物间的连线,并使闭合开关时,电压表或电流表不至于被烧坏。
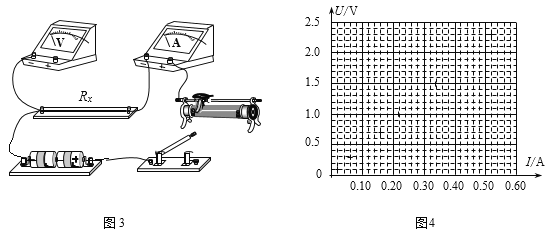
(4)该组同学在坐标纸上建立U—I坐标系,如图4所示,请在图4中标出测量数据坐标点,并描绘U─I图线。由图线得到金属丝的阻值Rx=_________Ω(保留两位有效数字)。
(5)根据以上数据可以估算出金属丝的电阻率约为_______Ω![]() m(填选项前的符号)。
m(填选项前的符号)。
A.1×10-2 B.1×10-3 C.1×10-6 D.1×10-8