题目内容
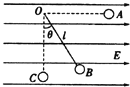
【题目】如图所示,一位同学做飞镖游戏,已知圆盘的直径为d,飞镖距圆盘为L,且对准圆盘上边缘的A点水平抛出,初速度为v0,飞镖抛出的同时,圆盘以垂直圆盘过盘心O的水平轴匀速运动,角速度为ω.若飞镖恰好击中A点,则下列关系正确的是( )

A. ![]()
B. ωL=π(1+2n)v0,(n=0,1,2,3,…)
C. 2dv02=L2g
D. dω2=gπ2(1+2n)2,(n=0,1,2, 3,…)
【答案】B
【解析】试题分析:飞镖做平抛运动的同时,圆盘上A点做匀速圆周运动,恰好击中A点,说明A点正好在最低点被击中,设时间为t,飞镖飞行时间t和圆盘转动的周期满足:t=nT+![]() ,(n=0,1,2、3…),由
,(n=0,1,2、3…),由![]() 和L=v0t得:ωL=π(2n+1)v0,(n=0,1,2、3…),故B正确,D错误.平抛的竖直位移为d,则d=
和L=v0t得:ωL=π(2n+1)v0,(n=0,1,2、3…),故B正确,D错误.平抛的竖直位移为d,则d=![]() gt2,联立解得dω2=
gt2,联立解得dω2=![]() gπ2(2n+1)2,2dv02=gL2,故AC错误.故选B.
gπ2(2n+1)2,2dv02=gL2,故AC错误.故选B.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目