��Ŀ����
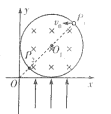
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵxOy�ĵ�һ�����ڴ��ڰ뾶R=![]() m��Բ����ǿ�ų����߽���x��y������У��Ÿ�Ӧǿ��B=2T������ֱ��ֽ��������ų�����Բ��O1��������ԭ��O��ֱ�߽��ų����߽���P1��P2���㣻���������ڴ�����y�����������ǿ�糡���糡ǿ��E=4��103V/m��һ�������������P����v0=1��103m/s�ij��ٶ�ƽ����x�Ḻ��������ų�������֪���ӵıȺ�Ϊ
m��Բ����ǿ�ų����߽���x��y������У��Ÿ�Ӧǿ��B=2T������ֱ��ֽ��������ų�����Բ��O1��������ԭ��O��ֱ�߽��ų����߽���P1��P2���㣻���������ڴ�����y�����������ǿ�糡���糡ǿ��E=4��103V/m��һ�������������P����v0=1��103m/s�ij��ٶ�ƽ����x�Ḻ��������ų�������֪���ӵıȺ�Ϊ![]() =2.5��102C/kg�������������ܵ���������
=2.5��102C/kg�������������ܵ���������
(1)������Բ���˶���Բ��O2���P2֮��ľ��룻
(2)���Ӵӵ�һ�ν���ų����ڶ��ν���ų���������ʱ�䡣��������ø��ű�ʾ��
���𰸡���1��2m����2��![]()
��������
(1)��ţ�ٵڶ����ɵ�
![]()
���
![]()
�����Ҷ���������Բ���˶���Բ��O2���P2֮��ľ���
![]()
�����ӽ���P2���뿪�ų���
(2)��ͼ��ʾ
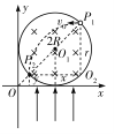
�ɼ��ι�ϵ��֪��������Բ����ǿ�ų�������![]() Բ���˶�����P2���뿪�ų�����P2��������
Բ���˶�����P2���뿪�ų�����P2��������
![]()
���Ӵӵ�һ�ν���ų����ڶ��ν���ų���������������ʱ�������![]() Բ���˶���ʱ�䡢�ų�������糡����֮�������ֱ���˶���ʱ�䡢��ǿ�糡�е�ʱ�䡣
Բ���˶���ʱ�䡢�ų�������糡����֮�������ֱ���˶���ʱ�䡢��ǿ�糡�е�ʱ�䡣
Բ���˶�ʱ��
![]()
�����˶�ʱ��
![]()
�ȱ���ֱ���˶�
![]()
����ʱ��
![]()
�����ʱ��
![]()

��ϰ��ϵ�д�
�����Ŀ