题目内容
【题目】如图所示,半径![]() 的
的![]() 光滑圆弧轨道固定在竖直平面内,过最低点的半径OC处于竖直位置,在其右方有一可绕竖直轴
光滑圆弧轨道固定在竖直平面内,过最低点的半径OC处于竖直位置,在其右方有一可绕竖直轴![]() 与圆弧轨道共面
与圆弧轨道共面![]() 转动的、内部空心的圆筒,圆筒半径
转动的、内部空心的圆筒,圆筒半径![]() ,筒的顶端与C点等高,在筒的下部有一小孔,离筒顶的高度
,筒的顶端与C点等高,在筒的下部有一小孔,离筒顶的高度![]() ,开始时小孔在图示位置
,开始时小孔在图示位置![]() 与圆弧轨道共面
与圆弧轨道共面![]() 。现让一质量
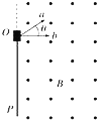
。现让一质量![]() 的小物块自A点由静止开始下落,打在圆弧轨道上的B点,但未反弹,在瞬间的碰撞过程中小物块沿半径方向的分速度立刻减为零,而沿圆弧切线方向的分速度不变。此后,小物块沿圆弧轨道匀速滑下,到达C点时触动光电装置,使圆筒立刻以某一角速度匀速转动起来,且小物块最终正好进入小孔。已知A点、B点到圆心O的距离均为R,AO、BO与水平方向的夹角
的小物块自A点由静止开始下落,打在圆弧轨道上的B点,但未反弹,在瞬间的碰撞过程中小物块沿半径方向的分速度立刻减为零,而沿圆弧切线方向的分速度不变。此后,小物块沿圆弧轨道匀速滑下,到达C点时触动光电装置,使圆筒立刻以某一角速度匀速转动起来,且小物块最终正好进入小孔。已知A点、B点到圆心O的距离均为R,AO、BO与水平方向的夹角![]() 均为
均为![]() ,不计空气阻力,g取
,不计空气阻力,g取![]() ,试求:
,试求:

![]() 小物块到达C点时的速度大小是多少?
小物块到达C点时的速度大小是多少?
![]() 圆筒匀速转动时的角速度是多少?
圆筒匀速转动时的角速度是多少?
![]() 要使小物块进入小孔后能直接打到圆筒的内侧壁,筒身长L到少为多少?
要使小物块进入小孔后能直接打到圆筒的内侧壁,筒身长L到少为多少?
【答案】(1)![]() m/s (2)
m/s (2)![]() 2,3,
2,3,![]() (3)1.25m
(3)1.25m
【解析】
![]() 根据自由落体运动求出小球运动到B点的速度,将B点的速度沿径向和切向分解,得出切向方向的速度,由小物块沿圆弧轨道匀速滑下,到达C点,求出小物块在C点的速度大小;
根据自由落体运动求出小球运动到B点的速度,将B点的速度沿径向和切向分解,得出切向方向的速度,由小物块沿圆弧轨道匀速滑下,到达C点,求出小物块在C点的速度大小;
![]() 小物块离开C点后做平抛运动,根据高度求出平抛运动的时间,抓圆筒在该段时间内转动的角度为
小物块离开C点后做平抛运动,根据高度求出平抛运动的时间,抓圆筒在该段时间内转动的角度为![]() 2,3,
2,3,![]() ,求出圆筒转动的角速度;
,求出圆筒转动的角速度;
![]() 根据圆筒的直径求出物块在圆筒中运行的时间,从而得出平抛运动的总时间,根据平抛运动竖直方向上的运动规律求出物体下降的高度,即筒身的至少长度。
根据圆筒的直径求出物块在圆筒中运行的时间,从而得出平抛运动的总时间,根据平抛运动竖直方向上的运动规律求出物体下降的高度,即筒身的至少长度。
![]() 根据
根据![]() 得:
得:
![]() ;
;
![]() ;
;
小物块沿圆弧轨道匀速滑下,所以![]()
即小物块到达C点时的速度大小是![]() ;
;
![]() 由
由![]() 得:
得:![]() ;
;
则:![]() 2,3,
2,3,![]() ;
;
即圆筒匀速转动时的角速度是为![]() 2,3,
2,3,![]() ;
;
![]() ;
;
![]() ;
;
即要使小物块进入小孔后能直接打到圆筒的内侧壁,筒身长L到少为![]() 。
。

练习册系列答案
相关题目