题目内容
3. 如图所示,一轻杆两端分别固定质量均为m的小球A和B,放置于光滑半径为R的半圆轨道中,A球与圆心等高,B球恰在半圆的最低点,然后由静止释放,求在运动过程中两球的最大速度的大小.
如图所示,一轻杆两端分别固定质量均为m的小球A和B,放置于光滑半径为R的半圆轨道中,A球与圆心等高,B球恰在半圆的最低点,然后由静止释放,求在运动过程中两球的最大速度的大小.
分析 对于两球组成的系统,只有重力做功,系统的机械能守恒,当整体的重心最低时重力势能最小,动能最大,两球的速度最大,此时杆水平,根据机械能守恒定律求解.
解答 解:当杆水平时,整体的重心最低,两球的速度最大,设为v.
以B点所在水平面为参考平面,根据机械能守恒定律得:
mgR=2mgR(1-cos45°)+$\frac{1}{2}•2m{v}^{2}$
解得 v=$\sqrt{(\sqrt{2}-1)gR}$
答:在运动过程中两球的最大速度的大小为$\sqrt{(\sqrt{2}-1)gR}$.
点评 本题将两球看成一个整体,明确重心最低时,速度最大是关键,同时要注意单个小球的机械能并不守恒,只有系统的机械能守恒.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
13.‘神舟七号”飞船绕地球运转一周需要时间约90min,“嫦娥二号”卫星在工作轨道绕月球运转一周需要时间约118min(“神舟七号”和“嫦娥二号”的运动都可视为匀速圆周运动). 已知“嫦娥二号”卫星距月球中心的距离约为“神舟七号”飞船距地球中心距离的$\frac{3}{11}$.根据以上数据可求得( )
| A. | 月球与地球的质量之比 | |
| B. | “嫦娥二号”卫星与“神舟七号”飞船的质量之比 | |
| C. | 月球与地球的第一宇宙速度之比 | |
| D. | 月球表面与地球表面的重力加速度之比 |
14.河宽100m,船在静水中速度为4m/s,水流速度是3m/s,则下列说法正确的是( )
| A. | 船过河的最短时间25 s | B. | 船可以垂直过河 | ||
| C. | 船渡河的时间可以为18s | D. | 船不可能垂直过河 |
11.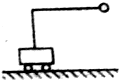 如图,小球用细线悬挂在光滑静止的小车上,细线呈水平位置,现无初速释放小球,下摆过程中( )
如图,小球用细线悬挂在光滑静止的小车上,细线呈水平位置,现无初速释放小球,下摆过程中( )
 如图,小球用细线悬挂在光滑静止的小车上,细线呈水平位置,现无初速释放小球,下摆过程中( )
如图,小球用细线悬挂在光滑静止的小车上,细线呈水平位置,现无初速释放小球,下摆过程中( )| A. | 线的拉力对小球不做功 | |
| B. | 合外力对小球不做功 | |
| C. | 细线拉力对小车做正功 | |
| D. | 小球和小车的总机械能、总动量均守恒 |
1.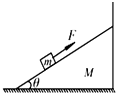 如图,斜面小车M静止在光滑水平面上,右边紧贴墙壁,若在M斜面上放一个物体m,物体恰好能沿着斜面匀速下滑,整个过程M始终静止不动.若给m一个沿斜面向上的力,使m恰好能沿着斜面匀速上滑则下面说法正确的是( )
如图,斜面小车M静止在光滑水平面上,右边紧贴墙壁,若在M斜面上放一个物体m,物体恰好能沿着斜面匀速下滑,整个过程M始终静止不动.若给m一个沿斜面向上的力,使m恰好能沿着斜面匀速上滑则下面说法正确的是( )
 如图,斜面小车M静止在光滑水平面上,右边紧贴墙壁,若在M斜面上放一个物体m,物体恰好能沿着斜面匀速下滑,整个过程M始终静止不动.若给m一个沿斜面向上的力,使m恰好能沿着斜面匀速上滑则下面说法正确的是( )
如图,斜面小车M静止在光滑水平面上,右边紧贴墙壁,若在M斜面上放一个物体m,物体恰好能沿着斜面匀速下滑,整个过程M始终静止不动.若给m一个沿斜面向上的力,使m恰好能沿着斜面匀速上滑则下面说法正确的是( )| A. | m匀速下滑时,M的受力个数一定是4个 | |
| B. | 在F作用下m匀速上滑时,M的受力个数一定是4个 | |
| C. | 在F作用下m匀速上滑时,墙壁对M的力为Fcosθ | |
| D. | 在F作用下m匀速上滑时,墙壁对M的力为零 |
8.一物体自空中自由下落,第1秒内下落了总高度的一半.那么,物体还要多长时间才落地( )
| A. | 1s | B. | 1.5s | C. | ($\sqrt{2}$-1)s | D. | $\sqrt{2}$s |
6.以下情景中,带下划线的物体可看成质点的是( )
| A. | 裁判员在跳水比赛中给跳水运动员评分 | |
| B. | 用GPS确定出租车在城市中的位置 | |
| C. | 在国际大赛中,乒乓球运动员王浩准备接对手发出的旋转球 | |
| D. | 研究“嫦娥一号”从地球到月球的飞行姿态变化 |
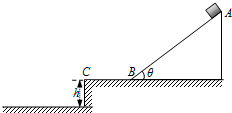 如图所示,光滑斜面AB与光滑水平面BC平滑连接.斜面AB长度L=3.0m,倾角θ=37°.一小物块在A点由静止释放,先后沿斜面AB和水平面BC运动,接着从点C水平抛出,最后落在水平地面上.已知水平面BC与地面间的高度差h=0.80m.取重力加速度g=10m/s2,sin37°=0.60,cos37°=0.80.不计空气阻力.求
如图所示,光滑斜面AB与光滑水平面BC平滑连接.斜面AB长度L=3.0m,倾角θ=37°.一小物块在A点由静止释放,先后沿斜面AB和水平面BC运动,接着从点C水平抛出,最后落在水平地面上.已知水平面BC与地面间的高度差h=0.80m.取重力加速度g=10m/s2,sin37°=0.60,cos37°=0.80.不计空气阻力.求