题目内容
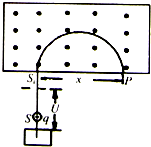 质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造原理如图所示.离子源S产生的各种不同正离子束(速度可看作为零),经加速电场(加速电场极板间的距离为d、电势差为U)加速,然后垂直进入磁感应强度为B的有界匀强磁场中做匀速圆周运动,最后到达记录它的照相底片P上.设离子在P上的位置与人口处S1之间的距离为x.
质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造原理如图所示.离子源S产生的各种不同正离子束(速度可看作为零),经加速电场(加速电场极板间的距离为d、电势差为U)加速,然后垂直进入磁感应强度为B的有界匀强磁场中做匀速圆周运动,最后到达记录它的照相底片P上.设离子在P上的位置与人口处S1之间的距离为x.(1)求该离子的比荷卫
| q | m |
(2)若离子源产生的是带电量为q、质量为m1和m2的同位素离子(m1>m2),它们分别到达照相底片上的P1、P2位置(图中末画出),求P1、P2间的距离△x.
(3)若第(2)小题中两同位素离子同时进入加速电场,求它们到达照相底片上的时间差△t(磁场边界与靠近磁场边界的极板间的距离忽略不计).
分析:(1)根据粒子在磁场中的运动半径,通过半径公式求出粒子的速度,再根据动能定理得出粒子的比荷.
(2)根据动能定理、半径公式求出粒子打到照相机底片上位置与入口处的距离,从而求出P1、P2间的距离△x.
(3)粒子在加速电场中做匀加速直线运动,在磁场中做匀速圆周运动,结合牛顿第二定律和运动学公式以及粒子在磁场中运动的周期公式求出从射出到打到底片上的时间,从而求出它们到达照相底片上的时间差△t.
(2)根据动能定理、半径公式求出粒子打到照相机底片上位置与入口处的距离,从而求出P1、P2间的距离△x.
(3)粒子在加速电场中做匀加速直线运动,在磁场中做匀速圆周运动,结合牛顿第二定律和运动学公式以及粒子在磁场中运动的周期公式求出从射出到打到底片上的时间,从而求出它们到达照相底片上的时间差△t.
解答:解:(1)粒子在磁场中做圆周运动的半径为r=
.
根据qvB=m
,解得v=
=
.
根据动能定理得,qU=
mv2
联立解得
=
.
(2)根据qU=
mv2
r=
,x=2r
解得x=2
,
则△x=2
(
-
).
(3)根据d=
at12,a=
解得t1=
.
粒子在磁场中运动的周期T=
.
则粒子运动的时间t=t1+
=
+
.
则△t=
+
-
-
.
答:(1)该离子的比荷为
=
.
(2)P1、P2间的距离△x=2
(
-
)
(3)它们到达照相底片上的时间差△t=
+
-
-
.
| x |
| 2 |
根据qvB=m
| v2 |
| r |
| qBr |
| m |
| qBx |
| 2m |
根据动能定理得,qU=
| 1 |
| 2 |
联立解得
| q |
| m |
| 8U |
| B2x2 |
(2)根据qU=
| 1 |
| 2 |
r=
| mv |
| qB |
解得x=2
|
则△x=2
|
| m1 |
| m2 |
(3)根据d=
| 1 |
| 2 |
| qU |
| md |
解得t1=
|
粒子在磁场中运动的周期T=
| 2πm |
| qB |
则粒子运动的时间t=t1+
| T |
| 2 |
|
| πm |
| qB |
则△t=
|
| πm1 |
| qB |
|
| πm2 |
| qB |
答:(1)该离子的比荷为
| q |
| m |
| 8U |
| B2x2 |
(2)P1、P2间的距离△x=2
|
| m1 |
| m2 |
(3)它们到达照相底片上的时间差△t=
|
| πm1 |
| qB |
|
| πm2 |
| qB |
点评:本题考查了带电粒子在电场中的加速和在磁场中的偏转,结合牛顿第二定律和运动学公式综合求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造原理如图所示,离子源S产生的各种不同正离子束(电量为q,速度可看作为零),经加速电场电压U加速后垂直进入有界匀强磁场,到达记录它的照相底片P上,设离子在P上的位置到入口处S1的距离为x,不计离子重力,则下列说法正确的是( )
质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造原理如图所示,离子源S产生的各种不同正离子束(电量为q,速度可看作为零),经加速电场电压U加速后垂直进入有界匀强磁场,到达记录它的照相底片P上,设离子在P上的位置到入口处S1的距离为x,不计离子重力,则下列说法正确的是( )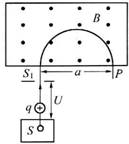 质谱仪是一种测定带电粒子质量和分析同位素的重要工具.它的构造原理如图所示,离子源S产生带电量为q的某种正离子,离子射出时的速度很小,可以看作是静止的,离子经过电压U加速后形成离子束流,然后垂直于磁场方向进入磁感应强度为B的匀强磁场,沿着半圆周运动而到达记录它的照相底片P上.实验测得:它在P上的位置到入口处S1的距离为a,离子束流的电流为I.请回答下列问题:
质谱仪是一种测定带电粒子质量和分析同位素的重要工具.它的构造原理如图所示,离子源S产生带电量为q的某种正离子,离子射出时的速度很小,可以看作是静止的,离子经过电压U加速后形成离子束流,然后垂直于磁场方向进入磁感应强度为B的匀强磁场,沿着半圆周运动而到达记录它的照相底片P上.实验测得:它在P上的位置到入口处S1的距离为a,离子束流的电流为I.请回答下列问题: 质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造原理如图所示,离子源S产生的各种不同正离子束(速度可看作为零),经加速电场加速后垂直进入有界匀强磁场,到达记录它的照相底片P上,设离子在P上的位置到入口处S1的距离为x,则下列判断正确的是( )
质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造原理如图所示,离子源S产生的各种不同正离子束(速度可看作为零),经加速电场加速后垂直进入有界匀强磁场,到达记录它的照相底片P上,设离子在P上的位置到入口处S1的距离为x,则下列判断正确的是( ) 质谱仪是一种测定带电粒子质量或分析同位素的重要设备,它的构造原理如图所示.离子源S产生的各种不同正离子束(速度可视为零),经MN间的加速电压U加速后从小孔S1垂直于磁感线进入匀强磁场,运转半周后到达照相底片上的P点.设P到S1的距离为x,则( )
质谱仪是一种测定带电粒子质量或分析同位素的重要设备,它的构造原理如图所示.离子源S产生的各种不同正离子束(速度可视为零),经MN间的加速电压U加速后从小孔S1垂直于磁感线进入匀强磁场,运转半周后到达照相底片上的P点.设P到S1的距离为x,则( )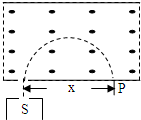 质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造原理如图所示,离子源S可以发出各种不同的正离子束,离子从S出来时速度很小,可以看作是静止的,离子经过加速电场加速后垂直进入有界匀强磁场(图中线框所示),并沿着半圆周运动而到达照像底片上的P点,测得P点到入口处S的距离为x?( )
质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造原理如图所示,离子源S可以发出各种不同的正离子束,离子从S出来时速度很小,可以看作是静止的,离子经过加速电场加速后垂直进入有界匀强磁场(图中线框所示),并沿着半圆周运动而到达照像底片上的P点,测得P点到入口处S的距离为x?( )