题目内容
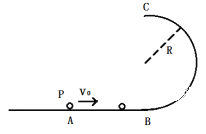
【题目】如图所示,光滑水平面AB与粗糙半圆轨道BC相切于B点,轨道半径为R=0.5m,小球P质量m1=0.2kg,以v0=9m/s的初速度向右运动,与静止在水平轨道上的Q小球发生弹性正碰,Q小球的质量m2=0.4kg,小球Q被碰后恰好能沿BC轨道到达C点,取g=10m/s2,
求:(1)碰后小球Q经过B点时对轨道的压力大小;
(2)小球Q沿轨道从B点运动到C点的过程中克服摩擦力所做的功。
【答案】(1)32.8N;(2)2.2J;
【解析】试题分析:
(1)由动量守恒定律和能量守恒定律求出Q球的速度,再根据牛顿第二定律求解在B点的压力;
(2) 从B到C,由动能定理和在C处的速度得出摩擦力做的功。
(1)由动量守恒有: ![]()
能量守恒得:![]()
联立以上两方程解得:![]()
小球Q在B点:![]()
解得![]() 由牛顿第三定律得,Q对轨道的压力
由牛顿第三定律得,Q对轨道的压力![]() ;
;
(2) 从B到C,由动能定理得
![]()
在C处:![]()
由以上两代入数据得![]() 。
。
点晴:本题为曲线运动与动量守恒定律、动能定理的综合应用典型题,解题的关键在于对过程和点的把握;运动过程的选择、受力分板的位置,会影响解题的难易程度。

练习册系列答案
相关题目