题目内容
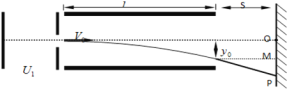
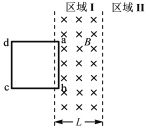
【题目】边长为L、电阻为R的正方形导线框位于光滑水平面内，线框的右侧区域I内存在宽度为L的有界匀强磁场，磁感应强度为B，方向垂直于水平面。线框在功率恒为P的外力作用下，ab边恰好向右匀速穿过磁场。ab边进入区域II后，立即受到与速度成正比的阻力作用，即Ff=kv，k为恒量。求：
（1）ab边在区域I内运动的速度v0；
（2）分析说明线框cd边在磁场中的运动情况；
（3）若cd边在穿过磁场的过程中，线框克服阻力做功为W，求线框中产生的焦耳热。
【答案】（1）v0=
；（2）见解析；（3）Q= 
W
【解析】
（1）电动势
E0=BLv0
电流强度
I0=
安培力
FA=BI0L=
ab边在磁场内匀速运动时，平衡
F=FA=
拉力功率
P=Fv0=
解出
v0=
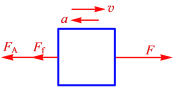
（2）cd边在磁场中，线框受力如图增加阻力后，合力向左，选向左为正方向，根据牛顿第二定律
FA+Ff -F=ma
求出加速度大小
a=
+
-
因v与a反方向，应减速运动，加速度随之也减小，故cd边在磁场内的过程中，线框做加速度减小的减速运动（最后可能匀速）
（3）线框速度为v时
FA=BIL=
因B、L、R均为恒量，故安培力与速度v成正比，而Ff也与速度v成正比，故两者的变化规律相同，必有
=
=
线框克服安培力做功
WA=W
线框中的焦耳热
Q=WA=W
练习册系列答案
相关题目
