题目内容
6. 如图所示,物体从O点由静止开始做匀加速直线运动,途经A、B、C三点,其中|AB|=2m,|BC|=3m.若物体通过AB和BC这两段位移的时间相等,则O、A两点之间的距离等于( )
如图所示,物体从O点由静止开始做匀加速直线运动,途经A、B、C三点,其中|AB|=2m,|BC|=3m.若物体通过AB和BC这两段位移的时间相等,则O、A两点之间的距离等于( )| A. | $\frac{9}{8}$ m | B. | $\frac{8}{9}$ m | C. | $\frac{3}{4}$ m | D. | $\frac{4}{3}$ m |
分析 根据某段时间内的平均速度等于中间时刻的瞬时速度,设相等的时间为T,求出B点的速度,从而得出A点的速度,根据连续相等时间内的位移之差是一恒量,求出加速度的大小,再根据速度位移公式求出0A间的距离.
解答 解:设物体通过AB、BC所用时间分别为T,则B点的速度为:
${v}_{B}=\frac{{x}_{AC}}{2T}=\frac{5}{2T}$,
根据△x=aT2得:a=$\frac{△x}{{T}^{2}}=\frac{1}{{T}^{2}}$,
则有:vA=vB-aT=$\frac{5}{2T}-\frac{1}{{T}^{2}}•T=\frac{3}{2T}$,
根据速度位移公式得,O、A两点之间的距离为:${x}_{OA}=\frac{{{v}_{A}}^{2}}{2a}=\frac{\frac{9}{4{T}^{2}}}{\frac{2}{{T}^{2}}}=\frac{9}{8}m$.故A正确,BCD错误.
故选:A.
点评 解决本题的关键掌握匀变速直线运动的公式以及推论,并能进行灵活的运用,有时运用推论求解会使问题更加简捷.

练习册系列答案
相关题目
16.某学习小组为探究导电溶液的电阻在体积相同时,电阻值与长度的关系.选取了一根乳胶管,里面灌满了盐水,两端用粗铜丝塞住管口,形成一段封闭的盐水柱.进行了如下实验: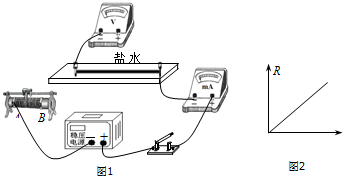
(1)该小组将盐水柱作为纯电阻,粗测其电阻约为几千欧.现采用伏安法测盐水柱的电阻,有如下实验器材供选择:
A.直流电源:电动势12V,内阻很小,额定电流为1A;
B.电流表A1:量程0~10mA,内阻约10Ω;
C.电流表A2:量程0~600mA,内阻约0.5Ω;
D.电压表V:量程0~15V,内阻约15kΩ;
E.滑动变阻器R1:最大阻值10Ω;
F.滑动变阻器R2:最大阻值5kΩ;
G.开关、导线等
在可供选择的器材中,应选用的电流表是A1(填“A1”或“A2”),应该选用的滑动变阻器是R2(填“R1”或“R2”).
(2)该小组已经完成部分导线的连接,请你在如图1实物接线图中完成余下导线的连接.
(3)握住乳胶管的两端把它均匀拉长,多次实验测得盐水柱长度L、电阻R的数据如下表:
为了研究电阻R与长度L的关系,该小组用纵坐标表示电阻R,作出了如图2所示的图线,你认为横坐标表示的物理量是L2.

(1)该小组将盐水柱作为纯电阻,粗测其电阻约为几千欧.现采用伏安法测盐水柱的电阻,有如下实验器材供选择:
A.直流电源:电动势12V,内阻很小,额定电流为1A;
B.电流表A1:量程0~10mA,内阻约10Ω;
C.电流表A2:量程0~600mA,内阻约0.5Ω;
D.电压表V:量程0~15V,内阻约15kΩ;
E.滑动变阻器R1:最大阻值10Ω;
F.滑动变阻器R2:最大阻值5kΩ;
G.开关、导线等
在可供选择的器材中,应选用的电流表是A1(填“A1”或“A2”),应该选用的滑动变阻器是R2(填“R1”或“R2”).
(2)该小组已经完成部分导线的连接,请你在如图1实物接线图中完成余下导线的连接.
(3)握住乳胶管的两端把它均匀拉长,多次实验测得盐水柱长度L、电阻R的数据如下表:
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 长度L(cm) | 20.0 | 25.0 | 30.0 | 35.0 | 40.0 | 45.0 |
| 电阻R(kΩ) | 1.3 | 2.1 | 3.0 | 4.1 | 5.3 | 6.7 |
11.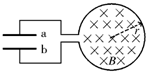 如图所示,有一匝接在电容器C两端的圆形导线回路,垂直于回路平面以内存在着向里的匀强磁场B,已知圆的半径r=5cm,电容C=20μF,当磁场B以4×10-2T/s的变化率均匀增加时,则( )
如图所示,有一匝接在电容器C两端的圆形导线回路,垂直于回路平面以内存在着向里的匀强磁场B,已知圆的半径r=5cm,电容C=20μF,当磁场B以4×10-2T/s的变化率均匀增加时,则( )
 如图所示,有一匝接在电容器C两端的圆形导线回路,垂直于回路平面以内存在着向里的匀强磁场B,已知圆的半径r=5cm,电容C=20μF,当磁场B以4×10-2T/s的变化率均匀增加时,则( )
如图所示,有一匝接在电容器C两端的圆形导线回路,垂直于回路平面以内存在着向里的匀强磁场B,已知圆的半径r=5cm,电容C=20μF,当磁场B以4×10-2T/s的变化率均匀增加时,则( )| A. | 电容器a板带正电,电荷量为2π×10-9C | |
| B. | 电容器a板带负电,电荷量为2π×10-9C | |
| C. | 电容器b板带正电,电荷量为4π×10-9C | |
| D. | 电容器b板带负电,电荷量为4π×10-9C |
16.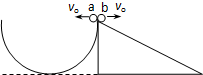 如图所示,a、b两个小球分别从半 轨道顶端和斜面顶端以大小相等的初速度同时水平抛出,已知半圆轨道的半径与斜面的竖直高度相等,斜面底边长是其竖直高度的2倍,则( )
如图所示,a、b两个小球分别从半 轨道顶端和斜面顶端以大小相等的初速度同时水平抛出,已知半圆轨道的半径与斜面的竖直高度相等,斜面底边长是其竖直高度的2倍,则( )
 如图所示,a、b两个小球分别从半 轨道顶端和斜面顶端以大小相等的初速度同时水平抛出,已知半圆轨道的半径与斜面的竖直高度相等,斜面底边长是其竖直高度的2倍,则( )
如图所示,a、b两个小球分别从半 轨道顶端和斜面顶端以大小相等的初速度同时水平抛出,已知半圆轨道的半径与斜面的竖直高度相等,斜面底边长是其竖直高度的2倍,则( )| A. | 一定是球先落在斜面上 | |
| B. | 可能是a球先落在半圆轨道上 | |
| C. | 当v0>$\frac{2\sqrt{10gR}}{5}$时,一定是a球先落到半圆轨道上 | |
| D. | 当v0<$\frac{4\sqrt{3gR}}{5}$时,一定是b球先落在斜面上 |
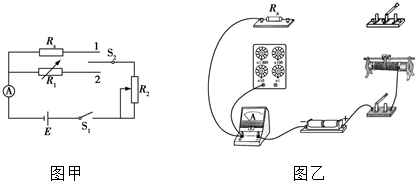
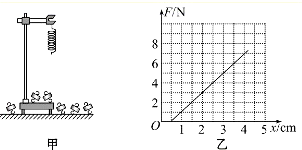
 某同学在做“探究弹力和弹簧伸长的关系”实验时,通过处理数据得到了如图1所示的F-x图象,其中F为弹簧弹力,x为弹簧长度.
某同学在做“探究弹力和弹簧伸长的关系”实验时,通过处理数据得到了如图1所示的F-x图象,其中F为弹簧弹力,x为弹簧长度.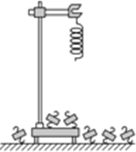 如图所示,用铁架台、弹簧和多个已知质量且质量相等的钩码探究在弹性限度内弹簧弹力与弹簧伸长量的关系.
如图所示,用铁架台、弹簧和多个已知质量且质量相等的钩码探究在弹性限度内弹簧弹力与弹簧伸长量的关系.