Question

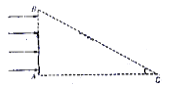
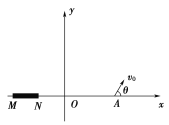
【题目】如图所示，在竖直平面内，第二象限存在方向竖直向下的匀强电场(未画出)，第一象限内某区域存在一边界为矩形、磁感应强度B0＝0.1 T、方向垂直纸面向里的匀强磁场(未画出)，A(m，0)处在磁场的边界上，现有比荷＝108 C/kg的离子束在纸面内沿与x轴正方向成θ＝60°角的方向从A点射入磁场，初速度范围为×106 m/s≤v0≤106 m/s，所有离子经磁场偏转后均垂直穿过y轴正半轴，进入电场区域。x轴负半轴上放置长为L的荧光屏MN，取π2＝10，不计离子重力和离子间的相互作用。

(1)求矩形磁场区域的最小面积和y轴上有离子穿过的区域长度；

(2)若速度最小的离子在电场中运动的时间与在磁场中运动的时间相等，求电场强度E的大小(结果可用分数表示)；

(3)在第(2)问的条件下，欲使所有离子均能打在荧光屏MN上，求荧光屏的最小长度及M点的坐标。

Answer 1

【答案】(1) m2 ，m，(2)×104 V/m，(3)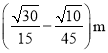，(－m，0)。

【解析】

(1)由洛伦兹力提供向心力，得

qvB＝

rmax＝＝0.1 m

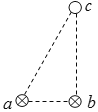
根据几何关系可知，速度最大的离子在磁场中做圆周运动的圆心恰好在y轴B(0，m)点，如图甲所示，离子从C点垂直穿过y轴。根据题意，所有离子均垂直穿过y轴，即速度偏向角相等，AC连线是磁场的边界。速度最小的离子在磁场中做圆周运动的半径：

rmin＝＝m

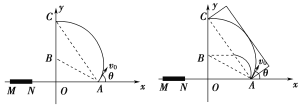
甲　　　　 　　　　　乙

速度最小的离子从磁场离开后，匀速前进一段距离，垂直y轴进入电场，根据几何知识，离子恰好从B点进入电场，如图乙所示，故y轴上B点至C点区域有离子穿过，且

BC＝m

满足题意的矩形磁场应为图乙中所示，由几何关系可知矩形长m，宽m，面积：

S＝m2；

(2)速度最小的离子从B点进入电场，离子在磁场中运动的时间：

t1＝T＝·

离子在电场中运动的时间为t2，则：

BO＝··

又因：

t1＝t2

解得：E＝×104 V/m；

(3)离子进入电场后做类平抛运动：

BO＝··

水平位移大小：

x1＝vB·t′1

同理：

CO＝··

水平位移大小：

x2＝vC·t′2

得：x1＝m，x2＝m

荧光屏的最小长度：

Lmin＝x2－x1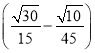＝m

M点坐标为(－m，0)。