题目内容
17.一颗质量为m的卫星围绕地球,在距离地球表面h高处,以周期T做匀速圆周运动,已知地球半径为R,引力常量为G,求:地球的质量M.分析 根据万有引力定律公式求出地球对卫星的万有引力大小.结合万有引力提供向心力求解.
解答 解:卫星作匀速圆周运动,根据万有引力充当向心力得
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
r=R+h
解得M=$\frac{{{4π}^{2}(R+h)}^{3}}{{GT}^{2}}$,
答:地球的质量是$\frac{{{4π}^{2}(R+h)}^{3}}{{GT}^{2}}$.
点评 万有引力定律常用方程有(1)星球表面的重力和万有引力相等;(2)环绕天体受到的万有引力提供向心力.这是解决这类问题常用的方程,要注意环绕天体运动半径的表述.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案
相关题目
7.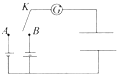 如图,电源A的电压为6v,电源B的电压为8V,当电键K从A转到B时,通过电流计的电量为1.4×10-5C;则电容器的电容为( )
如图,电源A的电压为6v,电源B的电压为8V,当电键K从A转到B时,通过电流计的电量为1.4×10-5C;则电容器的电容为( )
 如图,电源A的电压为6v,电源B的电压为8V,当电键K从A转到B时,通过电流计的电量为1.4×10-5C;则电容器的电容为( )
如图,电源A的电压为6v,电源B的电压为8V,当电键K从A转到B时,通过电流计的电量为1.4×10-5C;则电容器的电容为( )| A. | 2×10-5F | B. | 1.5×10-6F | C. | 6×10-6F | D. | 1×10-6F |
8.一质点做简谐运动,则下列说法中正确的是( )
| A. | 质点通过平衡位置时,速度为零,加速度最大 | |
| B. | 若位移为负值,则速度一定为正值,加速度也一定为正值 | |
| C. | 质点每次通过平衡位置时,加速度不一定相同,速度也不一定相同 | |
| D. | 质点每次通过同一位置时,其速度不一定相同,但加速度一定相同 |
5.下列关于物理学家的贡献的说法中,正确的是( )
| A. | 物理学家库仑利用扭秤实验发现了电荷间的相互作用规律 | |
| B. | 物理学家法拉第通过油滴实验精确测定了元电荷e的电荷量 | |
| C. | 物理学家密立根最早引入了电场概念,并提出用电场线表示电场 | |
| D. | 物理学家卡文迪许测出了静电力常量k |
12.图甲、图乙分别表示两种电压的波形,其中图甲所示电压按正弦规律变化,下列说法正确的是( )


| A. | 图甲表示交变电流,图乙表示直流电 | |
| B. | 两种电压的有效值都是220V | |
| C. | 图甲所示电压的瞬时值表达式为u=311sin100πt V | |
| D. | 图甲所示电压经原、副线圈匝数比为10:l的理想变压器变压后,原、副线圈电功率之比为10:l |
2.关于分子动理论和热力学定律,下列说法中正确的是( )
| A. | 空气相对湿度越大时,水蒸发越快 | |
| B. | 物体的温度越高,每个分子的动能都增大 | |
| C. | 第二类永动机不可能制成是因为它违反了热力学第一定律 | |
| D. | 两个分子间的距离由大于10-9m处逐渐减小到很难再靠近的过程中,分子间作用力先增大后减小到零,再增大 | |
| E. | 若一定量气体膨胀对外做功50J,内能增加80J,则气体一定从外界吸收130J的热量 |
9.下列说法正确的是( )
| A. | 增透膜的厚度等于入射光在真空中波长的$\frac{1}{4}$ | |
| B. | 观察者相对于频率一定的声源距离发生变化时,接收到声波的频率会发生变化 | |
| C. | 用标准平面检查光学平面的平整程度是利用光的偏振现象 | |
| D. | 在光的双缝干涉实验中,将入射光由绿光改为紫光,则条纹间隔变宽 |
7. 如图是街头变压器给用户供电的示意图.输入端接入的电压u=2200$\sqrt{2}$sin100πt(V),输出电压通过输电线输送给用户,输电线的电阻用R表示,理想变压器原、副线圈的匝数比为10:1,题中电表均为理想交流表,则下列说法正确的是( )
如图是街头变压器给用户供电的示意图.输入端接入的电压u=2200$\sqrt{2}$sin100πt(V),输出电压通过输电线输送给用户,输电线的电阻用R表示,理想变压器原、副线圈的匝数比为10:1,题中电表均为理想交流表,则下列说法正确的是( )
 如图是街头变压器给用户供电的示意图.输入端接入的电压u=2200$\sqrt{2}$sin100πt(V),输出电压通过输电线输送给用户,输电线的电阻用R表示,理想变压器原、副线圈的匝数比为10:1,题中电表均为理想交流表,则下列说法正确的是( )
如图是街头变压器给用户供电的示意图.输入端接入的电压u=2200$\sqrt{2}$sin100πt(V),输出电压通过输电线输送给用户,输电线的电阻用R表示,理想变压器原、副线圈的匝数比为10:1,题中电表均为理想交流表,则下列说法正确的是( )| A. | V2表的读数为220$\sqrt{2}$V | |
| B. | A1表的示数随A2表的示数的增大而增大 | |
| C. | 副线圈中交流电的频率为100Hz | |
| D. | 用户端闭合开关,则V2表读数不变,A1表读数变大,变压器的输入功率增大 |
 现有一只标有“6v、0.3A”的小灯泡,请从下述器材中选出一些器材,设计一个实验,能较为准确地测定小灯泡正常工作时的电阻值.
现有一只标有“6v、0.3A”的小灯泡,请从下述器材中选出一些器材,设计一个实验,能较为准确地测定小灯泡正常工作时的电阻值.