题目内容
【题目】如图所示,在xOy竖直平面内,Y轴的右侧有垂直纸面向外的匀强磁场B=0.4T和竖直向上的匀强电场E=2N/C。长为L=16m水平绝缘传送带AB以速度v0=3m/s顺时针匀速转动,右侧轮的轴心在Y轴上,右侧轮的上侧边缘B点的坐标是(0,h=8m)一个质量为M=2 g、电荷量为q=0.01C的小物块(可视为点电荷)以轻轻放在传送带左端,小物块与传送带之间的动摩擦因数μ=0.2,小物块从传送带滑下后,经过x轴上的P点(没画出),重力加速度g=10m/s2。求:
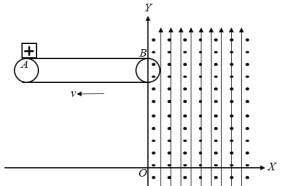
(1)P点的坐标;
(2)小物块从静止开始到经过x轴所用的时间;
(3)改变传送带匀速运行的速度,可让小物体从传送带上滑下后经过坐标原点O,那么要让小物块经过坐标原点,传送带运行速度的范围。
【答案】(1)(-3m,0)(2)8.65s (3)v≥8m/s。
【解析】
试题分析:(1)小物块在传送带做初速度为零的匀加速运动的加速度为:![]() ;
;
当小物块与传送带速度相等时,所用时间![]() ,这段时间内小物块的位移为:x1=
,这段时间内小物块的位移为:x1=![]() at2=2.25m<L=16m;
at2=2.25m<L=16m;
所以小物块先做匀加速运动,后做匀速运动,做匀速运动的时间为为:![]() ;
;
小物块从传送带下滑下进入y轴右侧后,因为电场力为:F=qE=0.02N,而mg=0.02N,且电场力方向竖直向上,与重力方向相反,所以合力为洛伦兹力;所以做匀速圆周运动,向心力由洛伦兹力提供,小物块的运动轨迹如图所示:
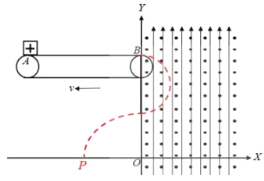
由向心力公式得,![]() ,解得:
,解得:![]() ,
,
运动时间为![]()
小物块离开磁场后,做平抛运动,运动时间为:![]() ;
;
水平方向上的位移为x2=v0t4=3m;
所以P点的坐标为(-3m,0);
(2)小物块从静止开始到经过X轴所用的时间t=t1+t2+t3+t4=8.65s;
(3)小物块要经过坐标原点0,它做匀速圆周运动的半径![]() ,洛伦兹力提供向心力,则有,
,洛伦兹力提供向心力,则有,![]() ,解得:
,解得:![]() ;
;
小物块在传送带上滑行的末速度是v1=8m/s,它在传送带上滑行的距离为![]() ,而L=16m,说明如果小物块在传送带上一直做匀加速运动,则小物块就会经过坐标原点O,所以传送带的速度v≥8m/s。
,而L=16m,说明如果小物块在传送带上一直做匀加速运动,则小物块就会经过坐标原点O,所以传送带的速度v≥8m/s。

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案