��Ŀ����
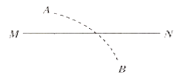
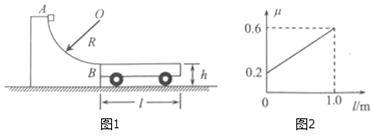
����Ŀ��ƽ��ֱ������ˮƽ���ֺ���б������ɣ������� L��0.5 m��PQ �Ƿֽ��ߣ���б�������Ϊ ����30����PQ �Ҳ��д�ֱ��б�����µ���ǿ�ų� B2��1 T��PQ �������Ŵ�ֱ ��ˮƽ�浫����δ֪����СҲΪ 1 T ����ǿ�ų� B1����ͼ��ʾ������ m��0.1 kg�������·�ĵ��� r��0.1 �� ����������ϸ�� ab �� cd ��ֱ���ڸõ����ϣ����� ab �˹⻬��cd ���뵼���Ķ�Ħ������Ϊ ����![]() ����˽��� R��0.1 �� �ĵ��衣��ʼʱab��cd ����ֹ�ڵ����ϡ��ֶ�ab ��ʩ��һˮƽ����ĺ㶨���� F��ʹ�������˶����� ab �������˶���λ��Ϊ x ʱ��ʼ���� ��ֱ���˶�����ʱ cd ��Ҫ��ʼ��б�������˶����Ա��־�ֹ�����پ� t��0.4 s ��ȥ���� F����� ab �˾�ֹ��ˮƽ�����ϡ����������е��� R �ķ�����Ϊ Q��1.0 J�������Ħ�������ڻ���Ħ ��������g��10 m/s2�����ƿ���������
����˽��� R��0.1 �� �ĵ��衣��ʼʱab��cd ����ֹ�ڵ����ϡ��ֶ�ab ��ʩ��һˮƽ����ĺ㶨���� F��ʹ�������˶����� ab �������˶���λ��Ϊ x ʱ��ʼ���� ��ֱ���˶�����ʱ cd ��Ҫ��ʼ��б�������˶����Ա��־�ֹ�����پ� t��0.4 s ��ȥ���� F����� ab �˾�ֹ��ˮƽ�����ϡ����������е��� R �ķ�����Ϊ Q��1.0 J�������Ħ�������ڻ���Ħ ��������g��10 m/s2�����ƿ���������
(1)�ж� B1 �ų��ķ���
(2)�ճ�ȥ���� F ʱ ab �˵��ٶ� v �Ĵ�С��
(3)�� ab �˵������ٶ� a �Ĵ�С�ͼ��ٹ����е�λ�� x �Ĵ�С��
���𰸡�(1)B1�ų��ķ���Ϊ��ֱ���£�(2) 1.5m/s��(3)25m/s2��1.8m
��������
(1)��������֪��ab�������˶���λ��Ϊxʱ��ʼ������ֱ���˶�����ʱcd��Ҫ��ʼ��б�������˶���cd���ܵ��İ�������б�����ϣ������ֶ���֪������cd���ĵ�����d��c������ab���ĵ���Ϊa��b��ab�����ܵ��İ�����ˮƽ���ң��������ֶ���B1�ų��ķ�����ֱ���£�
(2)��cd��
![]()
FA=B2IL
��
![]()
��ΪR=r����������R�ĵ���Ϊ2.5A
�ܵ���
I����5A
��·�ܵ���
R��=R��+r��0.15��
ab�����ĵ綯��
![]()
��ab��
E��B1Lv
���

(3)�����˶���λ��
x��=v��t=1.5��0.4 m =0.6m
ab�������˶�ʱ��
![]()
����ˮƽ����F=2.5N
�տ�ʼʱ���ٶ�Ϊ0����Ӧ�綯��Ϊ0��������Ϊ0����ab�ļ��ٶ����
![]()
ͨ������R��cd���ĵ�������ȣ�����ͨ��ab������һ�룬��·�����Ľ�����
![]()
���ݹ���ԭ��
F��x+x����=Q
��������
2.5����x+0.6��=6
���
x=1.8m